WILLナビ（ウィルナビ）─首都圏中学受験・塾・入試・学習情報サイト
協力／朝日小学生新聞・プレジデントFamily・東京出版・森上教育研究所・安田教育研究所・ワイワイネット、他
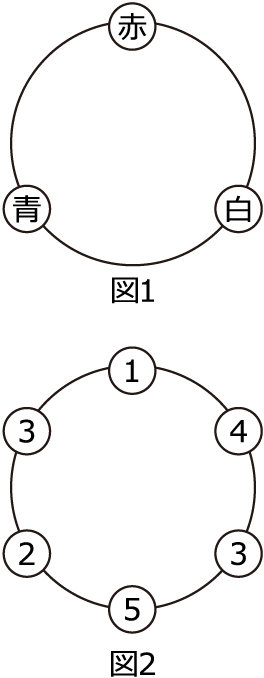図1のように，円周上に赤玉，青玉，白玉の3個を置き，それぞれの玉に1以上の整数を1つずつ書き入れます。
次に，以下の操作を行います。
操作：隣り合う2個の玉の間すべてに，緑玉を置き，それらの玉に隣り合う2個の玉に書かれた数の和を書く。
例えば，赤玉に1，青玉に2，白玉に3を書き，この操作を1回行うと，図2のようになり，6個のすべての玉に書かれた数の和は18になります。
この操作を繰り返し続けていきます。
次の各問いに答えなさい。
（1）赤玉に1，青玉に3，白玉に5を書き，この操作を2回行ったとき，12個のすべての玉に書かれた数の和はいくつですか。
（2）赤玉に1，青玉に3，白玉に5を書き，この操作を3回行ったとき，24個のすべての玉に書かれた数の和はいくつですか。
（3）赤玉に1，青玉に1を書き，この操作を4回行ったとき，すべての玉に書かれた数の和は1620でした。このとき，白玉に書いた数はいくつですか。
（4）この操作を1回以上行い，すべての玉に書かれた数の和が36になるように赤玉，青玉，白玉の3個に整数を書きます。この3個の玉の整数の書き方は全部で何通りですか。
（1） 実際に作業すると次のようになります。
図4の12個の数を合計して，81です。
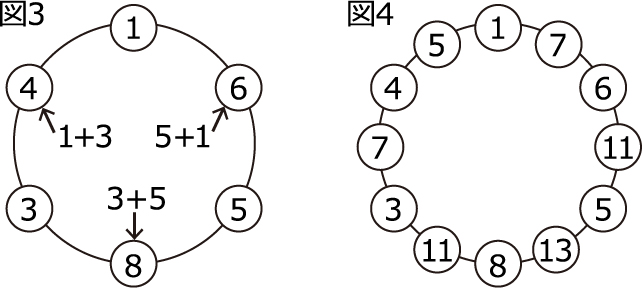
（2） はじめの和は9，図3の和は27ですから，次々と3倍になっていることが読み取れます。このことは，ある玉に書かれた数が，次の状態では3回足される（もとの玉と，両隣に新しく追加された玉）ことからも分かります。
よって，図4に操作をもう1回行ったときの和は，81×3＝243と求まります。
（3） 操作を4回行ったので，和ははじめの状態の3×3×3×3＝81（倍）になっています。はじめの和は1620÷81＝20ですから，白玉に書いた数は，20−（1＋1）＝18
（4） 36÷3＝12，12÷3＝4で4は3で割り切れません。よって，次の2パターンです。
（ア） はじめの和は12で1回操作を行った
（イ） はじめの和は4で2回操作を行った
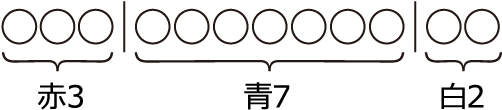（ア）のとき，右図のように○を12個並べ，間（両端は除く）の11か所から異なる2か所を選んで仕切りを入れます。3つの部分の○の個数を赤玉，青玉，白玉に書く整数にします。仕切りの入れ方を考えて，11×10÷2＝55（通り）
（イ）のとき，（1，1，2），（1，2，1），（2，1，1）の3通りです。
以上から，55＋3＝58（通り）
中学への算数
東京出版刊行
解き方のイメージを育て、思考力を鍛える！
詳しくはこちらから！
●編集方針●
最近の中学入試では、型にこだわらない新傾向問題が増えています。 これらは、ためしたり、かぞえたり、整理したり、場合を分けたり、 規則性を発見したり、グラフを書いたり、図形を動かしたり、 立体をいろいろとりあつかったり、というように、 単なる反復練習では解くことのできない、 数学的な発想力や思考力を要求される問題です。 それに応える力を育てることが本誌の最大の目標です。同時に、受験を離れたところでも、算数のおもしろさ、 楽しさを伝えていきます。
WILLナビTOPへ
WILLナビ120%活用法
トップページへ戻る
高校課程では習熟度別授業やコース分けが導入されていますので、問題を解ける喜びや数学の楽しさを味わえる環境が整っています。授業ではただ板書をノートに写すのではなく、自分で考えて正解を導く努力をして下さい。そうすれば大学生や社会人になったとき、数学を1つの手段として用いることができるようになり、更には数学そのものの魅力に気づくはずです。