WILLナビ（ウィルナビ）─首都圏中学受験・塾・入試・学習情報サイト
協力／朝日小学生新聞・プレジデントFamily・東京出版・森上教育研究所・安田教育研究所・ワイワイネット、他
図のような立方体X，直方体Yがたくさんあります。X，Yをすきまなく積み上げて1辺の長さが3cmの立方体ABCD-EFGHを作ります。
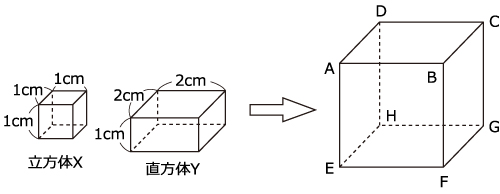
（1）Yをできるだけ多く使って，X，Yを積み上げて立方体ABCD-EFGHを作りました。このとき，XとYをそれぞれ何個使いましたか。また，作った立方体について，XとYの境界がわかるように解答用紙の図の点線を実線でなぞりなさい。ただし，すべてのYの一部の面がこの図から見えるように実線を書きなさい。
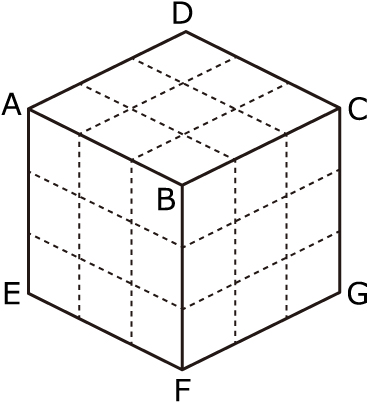
（2）（1）で作った立方体ABCD-EFGHをA，E，G，Cを含む平面で切断した後，ばらばらにしました。このとき，何個の立体に分かれましたか。
（3）（2）で分かれた立体のうち，体積が1cm3であるものの個数を求めなさい。
（1） 立方体ABCD-EFGHの体積は27cm3ですから，体積4cm3の直方体Yは，計算上は6個まで使えるのですが，その実例を発見できるかどうかが最大の難所です。
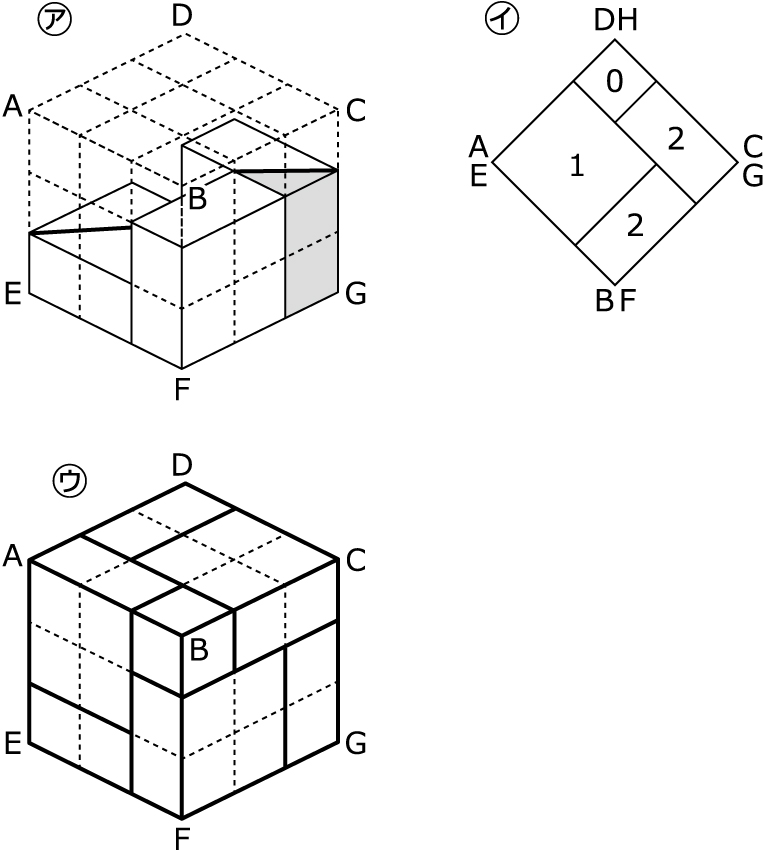
まず，3個の直方体Yを右図のアのように置きます。この時点で，真上から見てふさがっている段数は図イのようになるので，図アと合同な立体を，図アと点対称な位置関係になるように図アの上からかぶせれば，出来上がりです（図ウ，Yがふさいでいない部分がXで，Xは図ウの点Bから出る立方体の対角線上に3個並びます）。
（1）の答えは，X…3個，Y…6個，図ウ。
（なお，図ウのほか，これと鏡像の関係にある図も正解です。）
（2） 上の図アを見ると，3個のYのうち，A，E，G，Cを含む平面で2つに切断されるのは2個で，上からかぶせる3個のYについても同様です。また，3個のXのうち2つに切断されるのは，立方体の真ん中に位置する1個です。
よって答えは，（6＋3）＋2＋2＋1＝14（個）
（3） 上の図アを見ると，3個のYから切り取られる，体積が1cm3であるものは，網目部分の1個で，上からかぶせる3個のYについても同様です。また，切断されない2個のXの体積も1cm3です。
よって答えは，1×2＋2＝4（個）
中学への算数
東京出版刊行
解き方のイメージを育て、思考力を鍛える！
詳しくはこちらから！
●編集方針●
最近の中学入試では、型にこだわらない新傾向問題が増えています。 これらは、ためしたり、かぞえたり、整理したり、場合を分けたり、 規則性を発見したり、グラフを書いたり、図形を動かしたり、 立体をいろいろとりあつかったり、というように、 単なる反復練習では解くことのできない、 数学的な発想力や思考力を要求される問題です。 それに応える力を育てることが本誌の最大の目標です。同時に、受験を離れたところでも、算数のおもしろさ、 楽しさを伝えていきます。
WILLナビTOPへ
WILLナビ120%活用法
トップページへ戻る
論理的思考による問題解決能力が不可欠な現代社会においては希望進路にかかわらず、数学を学ぶ必要があります。そこで、どの生徒も無理なく学習を進められるように、複数学年でクラスを分割する少人数授業を実施し、また、小テストを進度に合わせて適宜（高２の演習授業では毎回）行い各自の理解度を確かめるなどの工夫をしています。