WILL�i�r�i�E�B���i�r�j����s�����w�E�m�E�����E�w�K���T�C�g
���́^�������w���V���E�v���W�f���gFamily�E�����o�ŁE�X�㋳�猤�����E���c���猤�����E���C���C�l�b�g�A��
WILL�i�r�i�E�B���i�r�j����s�����w�E�m�E�����E�w�K���T�C�g
���́^�������w���V���E�v���W�f���gFamily�E�����o�ŁE�X�㋳�猤�����E���c���猤�����E���C���C�l�b�g�A��



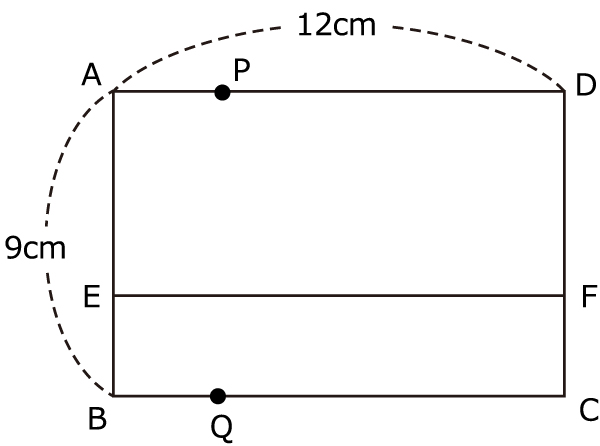 �@�}�̂悤�Ȓ����`ABCD������CAE��DF�͂ǂ����6cm�ł��B�_P�͕�AD�̏���C���b2cm�̑����ʼn��x���������܂��B�_Q�͕�BC�̏���CB����C�ɓ����Ƃ��͖��b2cm�̑����ŁCC����B�ɓ����Ƃ��͖��b1cm�̑����ʼn��x���������܂��BP��Q�����ꂼ��A,B���ɏo������Ƃ��C���̖₢�ɓ����Ȃ����B
�@�}�̂悤�Ȓ����`ABCD������CAE��DF�͂ǂ����6cm�ł��B�_P�͕�AD�̏���C���b2cm�̑����ʼn��x���������܂��B�_Q�͕�BC�̏���CB����C�ɓ����Ƃ��͖��b2cm�̑����ŁCC����B�ɓ����Ƃ��͖��b1cm�̑����ʼn��x���������܂��BP��Q�����ꂼ��A,B���ɏo������Ƃ��C���̖₢�ɓ����Ȃ����B
�i1�jP��Q���͂��߂ē�����A��B�������Ă���͉̂��b��ł����B
�i2�j����PQ�ƒ���EF����������_��R�Ƃ��܂��B���̂Ƃ��C���̖₢�ɓ����Ȃ����B
�@�@P��Q��18�b�ԓ����������Ƃ��CR�����������̂�͉�cm�ł����B�r���o�߂��L�����邱�ƁB
�A�@P��Q��5���ԓ����������Ƃ��CR�����������̂�͉�cm�ł����B�r���o�߂��L�����邱�ƁB
�i1�j�@P��A�ɖ߂�̂�
�@�@12×2÷2��12�i�b�j
���ƂŁCQ��B�ɖ߂�̂�
�@�@12÷2�{12÷1��18�i�b�j
���Ƃł��B
�@����āC12��18�̍ŏ����{������C36�b���ł��B
�i2�j�@�i1�j���36�b��1�����Ƃ��āCP��Q�̓����i��AB���牽cm����Ă��邩�j�����̃O���t�ɕ\���܂��B
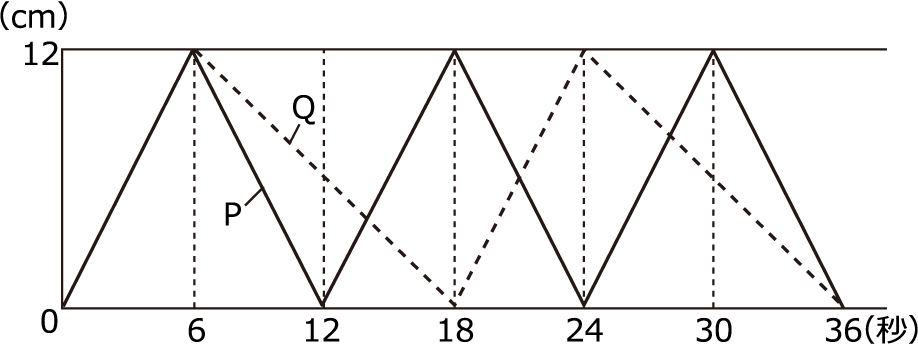
�@�@AE�FEB��6�F�i9−6�j��2�F1
�Ȃ̂ŁCER�̒����́CAP�̒�����BQ�̒�����2�F1�ɕ�����l�ɂȂ�܂��B
�@�O���t�̐܂�ڂł�ER�̒��������߂Ē����Ō��Ԃ��Ƃɂ��C���̃O���t�̑����̂悤�ɂȂ�܂��B
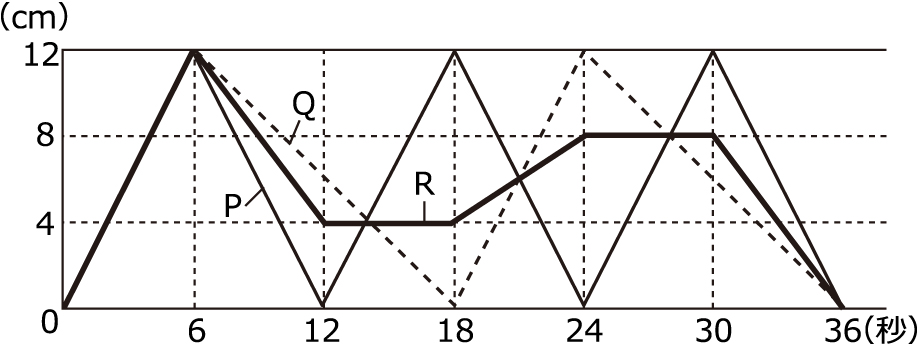
�@�@R�����������́C
�@�@0�`6�b �� 12cm
�@�@6�`12�b �� 12−4��8�icm�j
�@�@12�`18�b �� �����Ȃ�
�@����āC
�@�@12�{8��20�icm�j
�A�@18�`24�b �� 8−4��4�icm�j
�@�@24�`30�b �� �����Ȃ�
�@�@30�`36�b �� 8cm
�Ȃ̂ŁC1������R��
�@�@20�{4�{8��32�icm�j
�����܂��B
�@5���Ԃł́C
�@�@60×5÷36��8�i�����j�]��12�i�b�j
���C
�@�@32×8�{20��276�icm�j
�����܂��B
���w�ւ̎Z��
�����o�Ŋ��s
�������̃C���[�W����āA�v�l�͂�b����I

 �ڂ����͂����炩��I
�ڂ����͂����炩��I
���ҏW���j��
�ŋ߂̒��w�����ł́A�^�ɂ������Ȃ��V�X����肪�����Ă��܂��B �����́A���߂�����A����������A����������A�ꍇ������A �K������������A�O���t����������A�}�`��������A ���̂����낢��Ƃ肠��������A�Ƃ����悤�ɁA �P�Ȃ锽�����K�ł͉������Ƃ̂ł��Ȃ��A ���w�I�Ȕ��z�͂�v�l�͂�v���������ł��B ����ɉ�����͂���Ă邱�Ƃ��{���̍ő�̖ڕW�ł��B�����ɁA�𗣂ꂽ�Ƃ���ł��A�Z���̂������낳�A �y������`���Ă����܂��B
�@���w��RPG�Ɠ����ŁA���낢��ȍl����������Ƃ����X�L�����K�����A����炪�g����悤�ɂȂ��Ė��Ƃ����G��|���A�ǂ�ǂx���A�b�v���Ă����鋳�Ȃł��B�����Ջ��ŁA��������ɐ��w���x�����グ�Ă����܂��傤�I