WILL�i�r�i�E�B���i�r�j����s�����w�E�m�E�����E�w�K���T�C�g
���́^�������w���V���E�v���W�f���gFamily�E�����o�ŁE�X�㋳�猤�����E���c���猤�����E���C���C�l�b�g�A��
WILL�i�r�i�E�B���i�r�j����s�����w�E�m�E�����E�w�K���T�C�g
���́^�������w���V���E�v���W�f���gFamily�E�����o�ŁE�X�㋳�猤�����E���c���猤�����E���C���C�l�b�g�A��



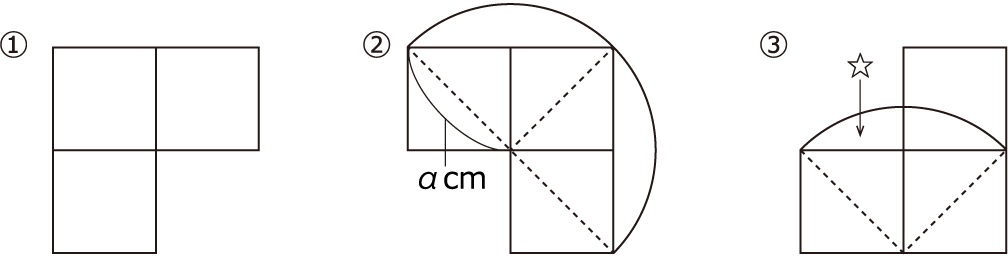
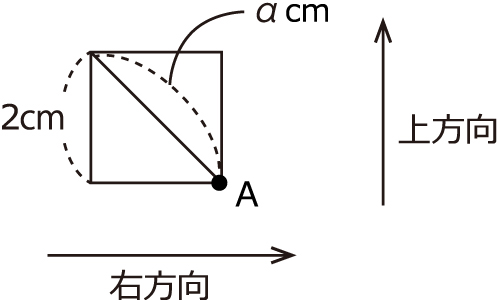 �@�E�̐}�̂悤�ɁC1�ӂ�2cm�̐����`�̒��_�ɓ_A������܂��B
�@�E�̐}�̂悤�ɁC1�ӂ�2cm�̐����`�̒��_�ɓ_A������܂��B
�@�܂��C���̒��ɁC�A�C�C�C�E�Ə����ꂽ�J�[�h��1�������v3�������Ă��܂��B�܂̒�����J�[�h��1�������āC�������J�[�h�ɂ���Ď��̃��[�����]���C���̐����`�����܂��B
�s���[���t
�A�c�����`���C������ς����܂������������2cm������
�C�c�����`���C������ς����܂������E������2cm������
�E�c�����`���C�_A�𒆐S�ɂ��Ď��v����90����]������
�@��x�������J�[�h�͑܂̒��������܂��B����������J��Ԃ��āC��̃��[���ɏ]�������`�����C�����`�̒ʂ������Ƃ̐}�`�̖ʐς��l���܂��B�Ⴆ�C�J�[�h��1��������A���������Ƃ��C�����`�̒ʂ������Ƃ̐}�`�̖ʐς�8cm2�ł��B
�@�������C���̐����`�̑Ίp���̒�����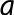 cm�Ƃ���Ƃ��C
cm�Ƃ���Ƃ��C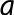 ×
×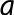 ��8�ƂȂ�܂��B�~������3.14�Ƃ��āC���̖₢�ɓ����Ȃ����B
��8�ƂȂ�܂��B�~������3.14�Ƃ��āC���̖₢�ɓ����Ȃ����B
�i1�j�J�[�h��2������܂��B���Ɏ��̃J�[�h���������Ƃ��C�����`�̒ʂ������Ƃ̐}�`�̖ʐς͂��ꂼ�ꉽcm2�ł����B
�@�@�A���C�@�@�A�@�E���E�@�@�B�@�E���A
�i2�j�J�[�h��3������܂��B�����E���C���A�̃J�[�h���������Ƃ��C�����`�̒ʂ������Ƃ̐}�`�̖ʐς͉�cm2�ł����B
�i3�j�J�[�h��3������܂��B�����`�̒ʂ������Ƃ̐}�`�̖ʐς�16cm2�ɂȂ�Ƃ��C�J�[�h�̈������͑S���ʼn��ʂ肠��܂����B
�i4�j�J�[�h��3������܂��B�����`�̒ʂ������Ƃ̐}�`�̖ʐς�17.14cm2�ɂȂ�Ƃ��C�J�[�h�̈������͑S����4�ʂ肠��܂��B���ɉ��̃J�[�h�������܂����B���ׂē����Ȃ����B
�i5�j�J�[�h��3������܂��B�����`�̒ʂ������Ƃ̐}�`�̖ʐς�15.42cm2�ɂȂ�Ƃ��C���ɉ��̃J�[�h�������܂����B
�i1�j�@���ꂼ��}�̂悤�ɂȂ�܂��B
�@�@�����`�̖ʐς�2×2��4�icm2�j�Ȃ̂ŁC 4×3��12�icm2�j
�A�@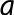 ×
×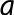 ×3.14÷2�{4
×3.14÷2�{4
�@��4×3.14�{4��16.56�icm2�j
�B�@�}�́��̖ʐς�
�@�@8×3.14×$\dfrac{\text{45}\,\,}{\text{360}\,\,}$−4÷2��1.14�icm2�j
�ł��B����āC
�@�@4×3�{1.14��13.14�icm2�j
�i2�j�@���̐}�̂悤�ɂȂ�܂��B
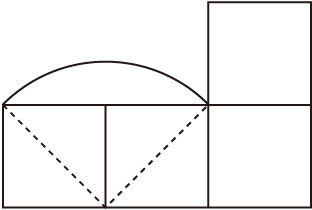
�@�����`4�Ɓ�2�Ȃ̂ŁC
�@�@4×4�{1.14×2��18.28�icm2�j
�i3�j�@�A���C����������Ԃ��Ƃ��C�͂��߁E1���E2���E�Ō�̐����`�͈قȂ�ʒu�ɂ���C�������`���o�Ă��܂���B�ʐς͕K��4×4��16�icm2�j�ɂȂ�܂��B
�@�ʐς�16cm2�ɂȂ�̂͂��̏ꍇ�����ŁC2×2×2��8�i�ʂ��j
�i4�j�@17.14��4×4�{1.14�Ȃ̂ŁC4�����̐����`�Ɂ���1�����ꍇ���ƍl�����܂��B
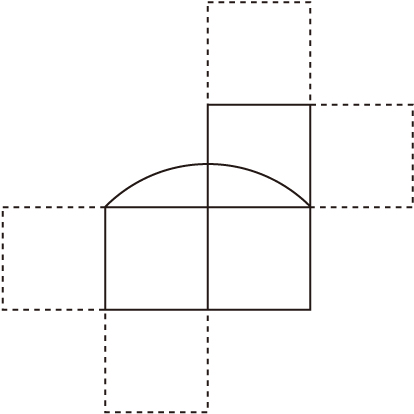
�@��̐}�̎������E���A�ƈړ������ꍇ�ŁC�����`��3�Ɓ���1����܂��B���̑O����A�܂����C�i�}�̓_���̐����`�j����������4�ʂ肪�����ɍ����܂��B
�i5�j�@15.42��16��菬�����̂ŁC�͂��߁E1���E2���E�Ō�̐����`�̂��������ʒu�ɗ�����̂��Ȃ���Ȃ�܂���B1��ڂ��E�ł͐����`�͉E�ɓ����̂ŁC�d�Ȃ邽�߂ɂ��E��2��ȏ�Ȃ���Ȃ�Ȃ����ƂɂȂ�܂��B
�@���̂悤�ȓ������ׂ܂��B�i1�j�A����C�E��2���Ƃ��ꂾ����16.56cm2�ƂȂ�傫�����܂��B
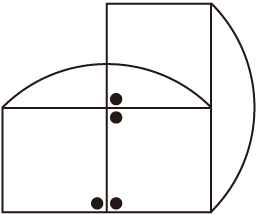
�@����āC�����E���A���E�C�E���C���E�Ɍ����܂��B���ׂ�ƁC�E���A���E�̂Ƃ��ɁC�}�̂悤�ɐ����`3�Ɓ�3�ƂȂ�
�@�@4×3�{1.14×3��15.42�icm2�j
�ŏ����ɍ����܂��i�}���́E��A�̈ʒu��\���܂��j�B
���w�ւ̎Z��
�����o�Ŋ��s
�������̃C���[�W����āA�v�l�͂�b����I

 �ڂ����͂����炩��I
�ڂ����͂����炩��I
���ҏW���j��
�ŋ߂̒��w�����ł́A�^�ɂ������Ȃ��V�X����肪�����Ă��܂��B �����́A���߂�����A����������A����������A�ꍇ������A �K������������A�O���t����������A�}�`��������A ���̂����낢��Ƃ肠��������A�Ƃ����悤�ɁA �P�Ȃ锽�����K�ł͉������Ƃ̂ł��Ȃ��A ���w�I�Ȕ��z�͂�v�l�͂�v���������ł��B ����ɉ�����͂���Ă邱�Ƃ��{���̍ő�̖ڕW�ł��B�����ɁA�𗣂ꂽ�Ƃ���ł��A�Z���̂������낳�A �y������`���Ă����܂��B
�@���w�ł͊�b�I�Ȍv�Z�͂�g�ɕt������悤�ɁA�v�Z�͐f�f�e�X�g���J��Ԃ����{���A�}�`�̏ؖ��ȂǂŔ��z�́E�\���͂��Ă��܂��B���R����͍��Z�̓��e����肵�A�e�P����ʂ��Ďv�l�͂��{���Ă����܂��B
�@�l�X�Ȋp�x��������߁A���ɑg�ݍ��킹�邱�Ƃɂ���Ė��������ق����Ă����B���w�̖��������Ȃ���A�_���I�v�l��g�ɕt���ė~�����ƍl���Ă��܂��B