
中学生になると、小学校と異なる勉強が始まります。算数の代わりに数学が始まりますし、英語の授業も本格的にスタートします。中学の英語の授業ではどんなことを学ぶのか、勉強についていけるのか、不安に感じている人もいるかもしれません。そんなみなさんに、勉強のコツや成績を伸ばすアイデアなどを紹介します。


仕事柄、いろいろなところで数学に関する話をする機会があるのですが、そんなとき、よく引き合いに出す話があります。
AさんとBさんは、T先生から次のように言われて240枚のシールを渡されました。
ゲームを5回行って、多く勝った人が240枚のシール全部を受け取りなさい。
そこで2人はゲームを始めましたが、2回目が終わったところでAさんの0勝2敗、3回目が終わったところでAさんの1勝2敗となりました。3回目にやっと勝つことができたものの、あとがない自分が不利だと思ったAさんは、ゲームの成り行きに目を光らせていたT先生がどこかへ行ってしまったのをよいことに、Bさんにある提案をしました。
以下は、2人の会話です。ただし、ゲームには引き分けはないものとします。また、ゲームの勝敗は偶然によって決まり、AさんとBさんのどちらが強いとか弱いとかは、ないものとします。
- A 「ねぇBさん、240枚を全部もらえるか、全然もらえないかじゃ、あまりにひどいと思わない? ここでゲームを打ち切って、2人でシールを分けることにしようよ。いまなら2人の勝ち数の比は1:2だから、この比で分けて、ぼくが80枚を、Bさんが160枚を受け取るってことで、どうだろう?」
- B 「2人で分けるのはかまわないけれど、1:2に分けるというのは納得がいかないわ。仮にあと2回ゲームをすると、4回目と5回目の勝ち負けは全部で4通り考えられるでしょう?」
さて、みなさんには、Bさんが「納得がいかない」わけを考えてもらいたいのですが、その手掛かりが、青字の部分です。
「4回目と5回目の勝ち負けは全部で4通り考えられる」のは、確かにその通りですね。その4通りのそれぞれについて、最終的にAさんの勝敗をまとめると、次のようになります。
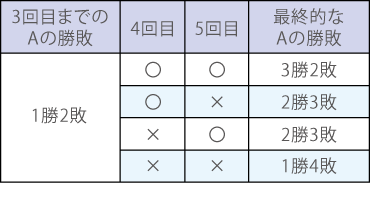
この表を見て、気づかれたでしょうか?
残り2回のゲームをしたとすると、表の4通りの結果は同じ確からしさで起こります。その4通りのうち、最終的に
Aさんが多く勝っている場合は、1通り
Bさんが多く勝っている場合は、3通り
ですね。
残り2回のゲームの結果、シールを全部もらえる可能性は、割合(比)で表すと、A:B=1:3なのです。
おそらくBさんは、
「これまでの勝ち負け(実績)で考えるのではなく、今後の勝ち負け(見込み)で考えるのが正しい」
と主張しているのでしょう。
この主張にしたがうと、2人のシールの取り分は、
| Aさん…240× | 1 | = | 60(枚)、 |
| 1+3 |
Bさん…240-60=180(枚)
となります。
Aさんは、「いやいや。見込みではなく実績で判断するべきだよ」と反論するかもしれませんが、それを論破するのは簡単です。
もし、2回目が終わった時点(Bさんの2勝0敗)でAさんと同じ提案をするならば、Bさんが240枚をすべて取ってしまうことになるからです。これは、どう考えてもおかしいですよね!
2回目が終わった時点で残り3回の結果を調べると、最終的に
Aさんが多く勝っている場合は、1通り
Bさんが多く勝っている場合は、7通り
となります(これは、みなさんも調べてね)から、2回目が終わった時点でゲームを打ち切ると、2人のシールの取り分は、
| Aさん…240× | 1 | = | 30(枚)、 |
| 1+7 |
Bさん…240-30=210(枚)
となります。
これは、確率の分野の「期待値」に関する話で、高校過程で学びます。しかし、話の内容は理解できたのではないでしょうか?
これから中学校に進学して、数学を学び始めるみなさんに、新たに学ぶ正負の数や文字式、方程式は重要な単元ですよ!と言うのは当たり前のことですが、実は、もっと大切なことがあります。
新たなことは“学ぶ”ことが必要ですが、学んだあとは、学んだことをもとにして、自分のアタマでとことん考えることが重要です。先の話のBさんの、「納得がいかない」という発言は、そうした学びから出てきたものなのでしょう。
みなさんがもし「すべてを学んで覚えてしまえばよい」式の学習を続ければ、数学は、みなさんの味方にはなってくれません。授業や本で必要最小限のことを学んだあとは、今度は自分をさらけ出して考えてください。そうすれば、心から数学を楽しめる日々が訪れることでしょう。

