|
 |
||||
|
■協力:東京出版 http://www.tokyo-s.jp/
毎月1日・11日・21日に問題解答を更新
|
|||||
|
6月21日/ハイレベル問題
【ギブアップ用解説】
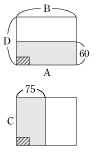
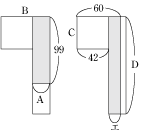
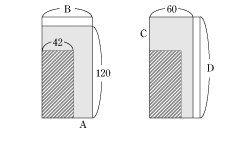
今回のポイントは、まず、体積が同じものに、ある等しい体積を加えたり引いたりしても、体積は同じままであるということ、体積や面積について、分かっている面積や長さを利用して、分からないところに比を出したり分からない面積や長さを求めることが出来るということです。
このことを上手く使えるようにするためには、図をよく見たり、書いたりして、どうすれば比を使いやすい図になるのか考えるクセをつけることが大事です。 あまり、出来なかった人は、以上のことを意識してこれから様々な問題に取り組んでみましょう。 |
|||||