|
 |
||||
|
■協力:東京出版 http://www.tokyo-s.jp/
毎月1日・11日・21日に問題解答を更新
|
|||||
|
6月11日/ハイレベル問題
【ギブアップ用解説】
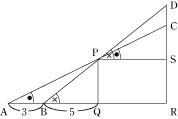
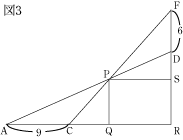
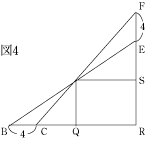
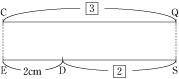
今回のポイントは、図形のなかで相似である部分をさがして、そこから相似を利用して、比で考えていくことです。
また、PA:AQ=CS:PSから、PQ×PS=AQ×CSとなるように、比では内側と外側の2つの数の積が等しいことを利用して計算することも重要です。 今回の問題は、この2つのポイントを理解すれば、解けるので、出来なかった人も、このことを理解したらもう一度解いてみましょう。 |
|||||