学力コンテスト

毎月1日・11日・21日に問題解答を更新

5月21日／ハイレベル問題

【ギブアップ用解説】

（1）	BとCが出会ってから離れるまで6秒かかっています。 BとCの列車の長さはどちらも90ｍなので、この6秒間でBとCが走った距離の合計は、90×2＝180ｍです。なので、BとCの速さの和は、180÷6＝30（ｍ／秒）となります。 BとCはどちらも同じ速さで走るので、答えは、30÷2＝15（m／秒）
（2）	AがBを追いこすのに35秒かかり、AがCとすれ違うのに5秒かかっています。また、BとCは長さも速さも同じなので、（AとBの速さの和）：（AとBの速さの差）＝35：5＝7：1となります。すると、図から15m／秒＝＜3＞、Aの速さ＝＜7＞−＜3＞＝＜4＞とわかるので、 Aの速さは、15÷3×4＝20（m／秒）また、AとCがすれ違うのにかかった時間は5秒なので、この間にAとCが走ったきょりの合計は（20＋15）×5＝175ｍであり、これはAとCの列車の長さの和です。よって、Aの長さは175−90＝85（ｍ）
（3）	Cは、Aと離れてから8秒後にBと出会っているので、AとCが離れたときには、Cの先頭とBの先頭は、（15＋15）×8＝240（ｍ）離れています。すると、図をみるとAの最後尾とBの先頭は、 240＋90＝330（ｍ）離れていることがわかります。 Aの先頭がイルカ水族館の看板の地点でBに追いつき、その35秒後にBと離れているので、求める時間は、35＋330÷（20−15）＝101（秒後）
（4）	（3）より、BとCが出会ったのは、Aの先頭がイルカ水族館の看板の地点を通ってから、101＋8＝109（秒後）また、BとCは同じ速さなので、Cがそこからイルカの看板の90ｍ手前まで進むのにも109秒かかります。よって、求める時間は、109×2＋90÷15＝224（秒後）

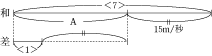
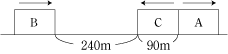
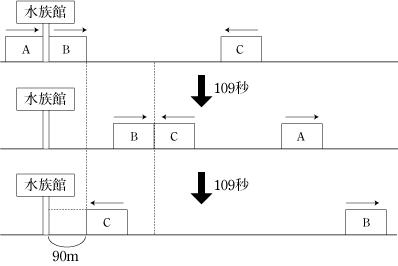
今回のポイントは、列車が他の列車とすれ違ったり、他の列車を追いこしたりするときに、どれだけの距離を通ったかをおさえたうえで、問題の状況をしっかりと整理することです。
まず、列車が他の列車とすれ違ったりするときの計算の仕方が分からなかった人は、基本問題にもどって、しっかりと基本が出来るようにしましょう。
なにごとも基本が出来なければ、応用は出来ません。
そして、基本は分かっていたけど、解けなかった人は、問題の状況を一つ一つ図に書いて整理の練習をしてみましょう。
状況の整理が上手に出来ていない人は、まず図を書く練習をすれば、そのうち状況の整理が上手に出来るようになるので、めんどうくさがらずにしっかりとやってくださいね。

ギブアップ・ウィンドウを閉じる