4月21日/ハイレベル問題
【解答・解説】

|
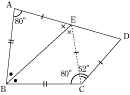
(1)
|
(ア)
CB=AB、BEは共通、角CBE=角ABEですから、三角形CBEとABEは合同です。
よって、角ECB=角EAB=80°とわかるので、答えは、132-80=52(度)
(イ)
三角形CBEとABEが合同であることから、CE=AEであることがわかります。
これと、AE=CDとから、三角形CDEは二等辺三角形とわかるので、
角CED=(180-52)÷2=64(度)
すると、
角BEC=角BEA=(180-64)÷2=58(度)
とわかるので、答えは、64+58=122(度)


|
|
(2)
|
角EAB=180-(74+32)=74(度)
角EAB=角BACということなので、これから、三角形ABCを辺ABを軸として折り返しできる三角形をABFとすると、D、A、Fは一直線になることがわかります。

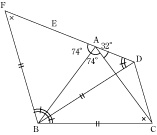

折り返しの性質から、
FB=CB……<1>、角AFB=角ACB……<2>です。
<1>とDB=CBとから、FB=DBとわかるので、
三角形FBDは二等辺三角形とわかります。よって、
角BFD=角BDF(=角ADB)
これと<2>とから、角ADB=角ACBがわかります。すると、
角ADB=角ABC
とから、結局、三角形ABCは、角ABC=角ACBの二等辺三角形であるということがわかります。
よって、角ADB=角ABC=(180-74)÷2=53(度)
すると、三角形ABDの内角に着目して
角ABD=180-(74+32+53)=21(度)
したがって答えは、53−21=32(度)
|
|



