|
 |
||||
|
■協力:東京出版 http://www.tokyo-s.jp/
毎月1日・11日・21日に問題解答を更新
|
|||||
|
5月1日/ハイレベル問題
【ギブアップ用解説】
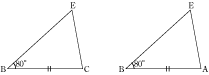
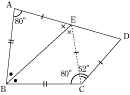
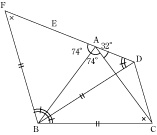
今回の学習のポイントは、まず、合同な三角形を見つけることです。
あせらなくとも、一つ一つ同じ長さの辺や角度に注意していくと、合同な三角形や、二等辺三角形などを見つけていくことが出来ます。 まずは、そのような地道な作業をしていくことで、合同な三角形などを見つける練習をしましょう。 そして、(2)のような問題では、自分で似たような形の三角形を書くことにより、合同な三角形などを見つけていくことが必要となります。 このような問題は、解けない人がほとんどなので、まずは、このような問題もあるのだということを覚えておきましょう。 図形の問題はあせらずに地道に練習していくことが大事ですよ。 |
|||||