学力コンテスト

■協力：東京出版 http://www.tokyo-s.jp/

毎月1日・11日・21日に問題解答を更新

4月21日／ハイレベル問題

【ギブアップ用解説】

（1）

下の図の様に、網目のかかっている正三角形と、その外側の二等辺三角形の面積を比べてみましょう。

すると、これらの面積が等しいことが分かりますね。
よって、正六角形を面積の等しい三角形に分割すると下の図のようになります。

この図より、答えは

倍であると分かります。

（2）

まずは、三角形ABFの面積について、下の図の様に正六角形を分割して考えてみます。

すると、三角形ABFの面積は正六角形の面積の

倍であることが分かります。

さらに、下の図を見ると、三角形AGLの面積は三角形ABFの面積の

＝

となります。

よって、A,B,C,D,E,Fを頂点とする６個の三角形の面積の和は、

もとの正三角形の面積の

となります。

一方、六角形GHIJKLも正六角形で、その内部にある網目部分の面積の和は、

（1）と同じで、正六角形GHIJKLの

です。

よって答えは

＋(1−

)×

＝

（倍）

（3）

下図の六角形PQRSTUも正六角形ですから、その内部にある網目部分の面積の和は、

正六角形PQRSTUの

です。

一方、三角形APUの面積は、ABFの

＝

ですから、

A､B､C､D､E､Fを頂点とする6個の三角形の面積の和も、もとの正六角形の面積の

です。

よって答えは、

+(1−

)×

＝

（倍）

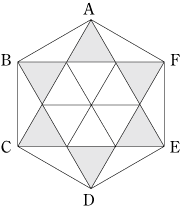
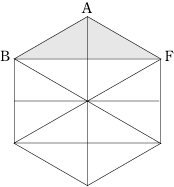
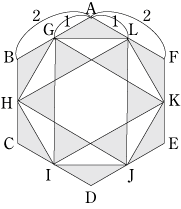
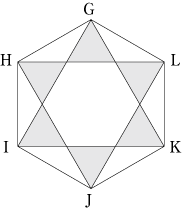
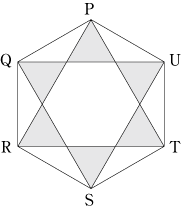
今回のポイントは、正六角形をさまざまな同じ面積の三角形に分割して考えることです。
また、（２）（３）では、正六角形の中にさらに正六角形があることに気付くことも大事です。
面積に関する問題で、同じ面積の図形に分割して考える問題はよくありますが、正六角形がその代表例です。
まずは、この問題をしっかり復習して、正六角形になれましょう！

ギブアップ・ウィンドウを閉じる