|
 |
|||||||||
|
■協力:東京出版 http://www.tokyo-s.jp/
毎月1日・11日・21日に問題解答を更新
|
||||||||||
|
4月11日/ハイレベル問題
【ギブアップ用解説】
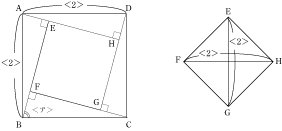
今回のポイントは、まず(1)では、面積をそれぞれの直角三角形と正方形EFGHに分けて考えられたかどうか。
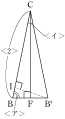
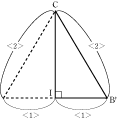
そして、(2)では、合同な三角形を2つくっつけて、その中から正三角形の半分の形をみつけられるかどうか。 これらがポイントとなります。 特に(2)は、とても難しい問題でしょう。 (2)のような難しい問題を解けるようにするためには、このような難しい問題を答えを見てしっかりと復習して定着させることが大事です。 はじめは解けなくても、さまざまな図形の問題の解き方を定着させていけば、テストのときでも解けるようになっていくので、あせらずにしっかりと復習してくださいね。 |
||||||||||