学力コンテスト

■協力：東京出版 http://www.tokyo-s.jp/

毎月1日・11日・21日に問題解答を更新

3月1日／ハイレベル問題

【ギブアップ用解説】

（1）

□＋2

□＋62

＝

になるとき、分母と分子の関係を線分図に表すと、下のようになります。

この図から、＜1＞＝60÷4＝15とわかるので、
□＝15×3-2＝43

□＋2

□＋62

＝

になるときも同じように考えて、線分図に表すと、下のようになります。

＜1＞＝60÷（7-4）＝20より、□＝20×4-2＝78
よって答えは、43から78までの整数の個数を求めて、
78-（43-1）＝36（通り）

（2）

□＋2

□＋62

＝

になるときは、同じように線分図で考えて、

＜1＞＝60÷（11-3）＝7.5より、□＝7.5×3-2＝20.5

□＋2

□＋62

＝

になるときも同様に、線分図で考えて、

＜1＞＝60÷（8-3）＝12より、□＝12×3-2＝34
ここで、（1）より、□に入る数が大きくなるほど分数の値も大きくなり、
□に入る数が小さくなるほど分数の値も小さくなることがわかるので、

より大きくなるのは、□が20.5より大きいとき、

3 8	より小さくなるのは、□が34未満のとき

であることがわかります。
以上から、答えは、21以上33以下の整数の個数を求めて、
33-（21-1）＝13（通り）

（3）

約分して

□＋2

□＋62

＝

になったとすると、下の図から、

（n-1）が60の約数であることがわかります。
ただし、＜1＞が3以上なので、60の約数のうちで、20以下が条件に合います。

６０の約数は、１，２，３，４、５，６，１０，１２，１５，２０，３０，６０の１２個です。
この中で、２０以下の約数は１０個あります。
よって、答え、１０通り

（4）

約分できなくなるまで約分して

□＋2

□＋62

＝

（mは奇数）になったとすると、

（m-2）が60の約数です。ただし、（m-2）は奇数なので、20以下の奇数でなければいけません。

60の約数のうちで奇数は、1、3、5、15の4個で、どれも20以下なので条件に合います。
よって、答えは、4通りです。

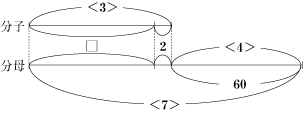
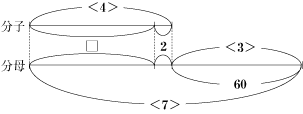
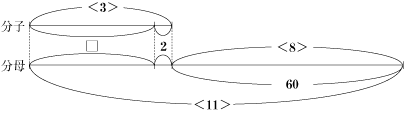
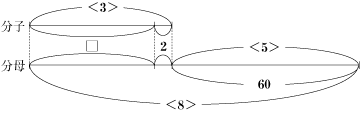
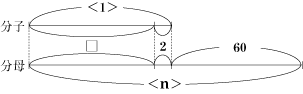
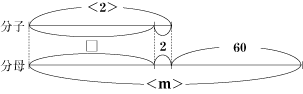
今回のポイントは、まず分子と分母の差に注目することです。
なぜなら、分子や分母の数が変化しても、差はかならず６０になるからです。
そのことに気付いて、分子と分母を比を使って考えると解けるでしょう。
また、ここで線分図を使うと比について考えやすくなります。
分子と分母の差が６０から変化しないことに始め気付かなくても、線分図などを書いて問題を整理して考えると、解き方の糸口が分かるはずです。まずは、図を書いて考える習慣をつけるようにしましょう。

ギブアップ・ウィンドウを閉じる