学力コンテスト

毎月1日・11日・21日に問題解答を更新

2月21日／ハイレベル問題

【ギブアップ用解説】

（1）	まず、どのような折りたたみ方があるのか考えてみましょう。実際に紙や折り紙などを使いながら考えてみると分かりやすいと思いますよ。始めに、＜1＞と＜2＞の間の折り目について、折りたたみ方を考えます。このように、＜2＞が上になるように折るか、＜2＞が下になるように折るかの２通りしかありません。さらに、＜2＞と＜3＞の間の折り目について、折りたたみ方を考えてみましょう。これも、＜3＞が上になるように折るか、下になるように折るかの２通りしかありません。このように、それぞれの間の折りたたみ方は、大きい番号が一番上になるように折るか、一番下になるように折るかの２通りとなります。さて、＜1＞から＜6＞までの折りたたみ方について考えましょう。折り目は、＜1＞と＜2＞の間、＜2＞と＜3＞の間、＜3＞と＜4＞の間、＜4＞と＜5＞の間、＜5＞と＜6＞の間の５ヶ所あります。このうち、＜5＞と＜6＞の間は、＜6＞が一番上になるように折ると決まっています。そして、他の４つの折り目については、それぞれ大きい番号が上になるように折るか下になるように折るかの２通りの折り方があります。よって、答えは２×２×２×２＝１６通りです。
（2）	（ア）実際に書いてみましょう。
	（イ）これも、まずは実際に書いてみましょう。＜5＞が上から２番目にあるような折り方は下のようになります。これから答えは、下のようになります。
（3）	長方形を６等分したときの折り方は（１）より１６通りあります。そして、これらの折り方は（２）で全て書かれています。よって、（２）の（ア）と（イ）をまとめれば答えです。答えは下のようになります。
（4）	まず、＜6＞が上から何番目にあるのか考えてみましょう。＜1＞から＜5＞まで折りたたんだ後、＜6＞が一番下になるように折り、さらに、＜7＞が一番上になるように折る場合がまずあります。そして、＜1＞から＜5＞まで折りたたんだ後、＜6＞が一番上になるように折り、さらに、＜7＞が一番上になるように折る場合もあります。他の場合はありません。つまり、＜6＞が上から７番目にあるときと、上から２番目にあるときとで場合分けして考えることが出来ます。（ウ）＜6＞が上から７番目にあるような折り方は下のようになります。（エ）＜6＞が上から２番目にあるときは、（３）の場合が１マス分だけずれることになります。よって、答えは下のようになります。

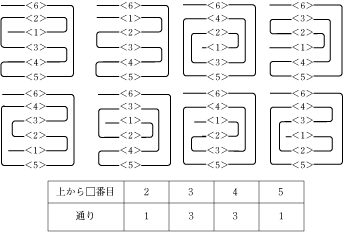
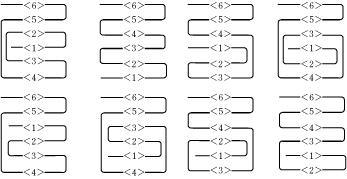
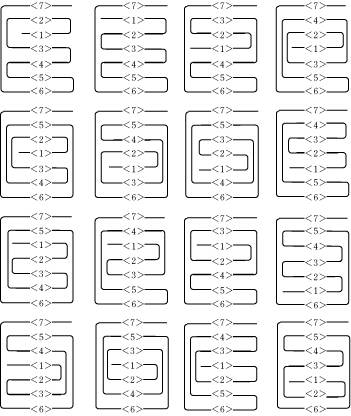
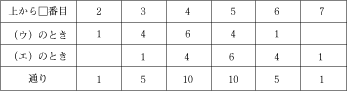
今回の問題では、まず、それぞれの折り目の折り方が何通りあるのか考えてみることです。
これを考えるためには、まず実際に自分で書くなり、紙を折るなりして具体的に確かめていくことが大事です。
自分で実際に試してみて、何通りあるのか予測をしてみて確かめることが大事なんですよ。
また、具体的に書いたりしたものから何か規則性を発見してみようとすると、さらに力がつきますよ。
例えば、（４）では、＜6＞が上から７番目にあるときと、上から２番目にあるときの２通りがありますが、これは（３）でも似たことが考えられます。
＜5＞が一番下にあるときと、上から２番目にあるときの２通りしかないんです。
これは、他の場合でも当てはまります。
このように、実際に書くことから何か規則を見つけようとすることは、算数力を伸ばすのに大事な姿勢なので、みなさんも心がけてみると良いでしょう！！

ギブアップ・ウィンドウを閉じる