|
 |
|||||||
|
■協力:東京出版 http://www.tokyo-s.jp/
毎月1日・11日・21日に問題解答を更新
|
||||||||
|
2月1日/ハイレベル問題
【ギブアップ用解説】
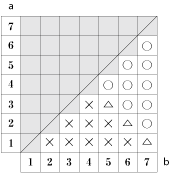
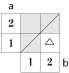
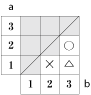
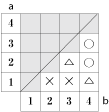
今回のポイントは、図や表を書いてみて、なにか規則がないのかと考えてみることです。
(2)の問題の場合、全ての○の個数を数えても大丈夫ですが、解答のように工夫した方が早く答えが出せます。
そのためには、表を2つ3つ書いてみて、○と×の数が同じではないのかと予想して、たしかめてみることです。 ときには予想が外れることもありますが、答えを予想してたしかめる練習を繰り返していると自然と算数の力が身についてきますよ! これからも、ぜひやってみたください。 |
||||||||