学力コンテスト

■協力：東京出版 http://www.tokyo-s.jp/

毎月1日・11日・21日に問題解答を更新

1月21日／ハイレベル問題

【ギブアップ用解説】

（1）

まずは、どのような形になるのかを考えましょう。t=0のとき、図1のようになるので、答えは
(6×6÷2)×6÷3=36cm³
t=6のとき。
図2のようになります。
ここで、四面体ＡＥＰＲ，四面体ＡＤＱＲ、四面体ＲＰＧＱ，四面体ＡＢＱＰに注目すると、これらは全てｔ＝０と合同な四面体だと分かります。
よって、求める体積は立方体ＡＢＣＤ－ＥＦＧＨから、
t=0のときと合同な四面体を4個切り落としたものなので、求める体積は、
6×6×6－36×4=72cm³

（2）

(ア)	P,Q,Rはそれぞれ辺BF,DC,EHのまん中にくるので、答えは図3の太線の正六角形になります。

(イ)	（ア）でえがいた正六角形に図のように点Ｓ、Ｔ、Ｕをとり、正六角形の中心に点Ｏをとります。すると、三角形ＯＱＲ、三角形ＵＱＲ，三角形ＯＰＲ，三角形ＴＰＲ，三角形ＯＰＱ、三角形ＳＰＱは全て合同な三角形となります。三角形ＰＱＲ＝三角形ＯＰＱ＋三角形ＯＰＲ＋三角形ＯＱＲなので、求める面積は12倍となります。

(ウ)

図3の正六角形の1辺の長さを1とすると、図1の正三角形の1辺の長さは2です。
ここで、図3の正六角形を3本の対角線で合同な6個の正三角形に分割してみます。

すると、図３には長さ１の正三角形が６つあり、図１には長さ２の正三角形が１つあります。
また、長さ２の正三角形と長さ１の正三角形の面積の比は２×２：１×１＝４：１です。
このことから、図１の正三角形と図３の正三角形の面積比が４×１：１×６＝４：６とわかるので、
(イ)から、答えは、

(6×

)÷4=

(倍)

(エ)

立体の断面ＡＣＧＥを用いて考えます。
Aから、t=0のときの三角形PQR(=三角形BDE)と、t=3のときの正六角形に垂直な線を引くと、右図のAK、ALになります。
これから、t=3のときと、t=0のときの高さの比が、AL：AK=3：2とわかるので、(1)と(ウ)を利用して、

答えは、36×

=40.5cm³

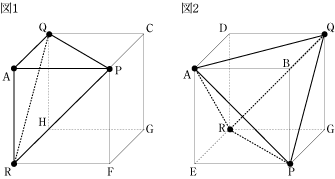
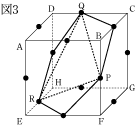
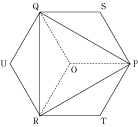
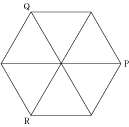
今回の問題は難しいように見えて、解き方の一つ一つは難しいものではありません。
まず、大事なことは図を書いて、目で理解できるものにして考えてみることです。
そして、一つ一つを丁寧に考えれば答えは出てくるでしょう。
実際の入試のときでも、難しい問題は特に図を書いてみましょう。
はじめは解けないと思った問題でも解けることがあるでしょう。
それでは、最後まであきらめずに入試を頑張って下さい !!

ギブアップ・ウィンドウを閉じる