(ア)
三角形BPTの面積は三角形PABの面積と等しいので、三角形ABCの面積とも等しくなります。正四面体の底面を三角形ABCと見ると、V-BPTと正四面体の高さの比は、VB:DB=2:1ですから、答えは2倍です。
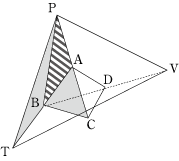
下図から、三角形BUVの面積は三角形BCDの面積の4倍であることがわかります。正四面体の底面を三角形BCDと見ると、T-BUVと正四面体の高さの比は、TB:AB=1:1ですから、答えは4倍です。
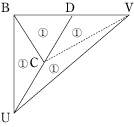
(イ)
残りの2つの四面体B-PTU、B-PUVもそれぞれ、頂点をU、底面を三角形BPTとする四面体U-BPT、頂点をP、底面を三角形BUVとする四面体P-BUVと見ることができます。
U-BPTと正四面体の底面積は等しく、高さの比は、UC:DC=1:1ですから、U-BPTの体積は正四面体と等しくなります。
P-BUVと正四面体の底面積の比は4:1で、高さの比は、PC:AC=2:1ですから、P-BUVの体積は正四面体の、4×2=8(倍)です。
以上から答えは、2+4+1+8=15(倍)



