|
 |
|||||||||||
|
■協力:東京出版 http://www.tokyo-s.jp/
毎月1日・11日・21日に問題解答を更新
|
||||||||||||
|
1月11日/ハイレベル問題
【ギブアップ用解説】
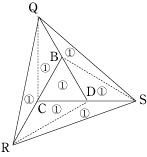
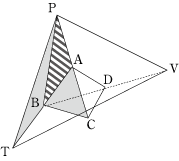
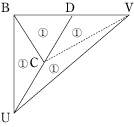
今回の問題のポイントは四面体の体積が底面積と高さに比例するということです。
四面体の体積は底面積×高さ÷3なので、底面積が2倍3倍と増えれば、体積も2倍3倍となっていきます。高さに対しても同じです。 そして、もう一つの大事なポイントは、四面体には4つの面がありますが、そのうち1つどの面を底面としても計算が出来ることです。なので、今回のように工夫次第で簡単に計算が出来るようになります。 また、今回の底面積の比の計算は基本的なものなので、間違えた人はしっかりと復習して下さい。 |
||||||||||||