■協力：東京出版 http://www.tokyo-s.jp/
毎月1日・11日・21日に問題解答を更新
12月21日／ハイレベル問題
【ギブアップ用解説】
（1）
図形の問題では、補助線を引くと分かり易くなることが多いです。
特に、この様な問題の場合、図のように補助線を引くと解ける場合が多いです。
また、下図のように点Xを通る各辺に平行な線を引き、交差に記号をつけると、
AB=FB+HF+AH…………＜3＞
であることがわかります。

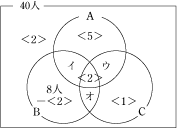
chart2.gif

ここで、四角形FBDXとAHXEは平行四辺形ですから、FB=XD、AH=EXより、＜3＞は、
AB=XD+EX+HF=a+EX+HF
となります。さらに、
三角形EXGとABCは相似形で、
EX:XG=AB:BCより、
EX=XG× AB
1px_999.gif
BC
 =a× AB
1px_999.gif
BC
三角形HFXとABCは相似形で、
HF:HX=AB:ACより、
HF=HX× AB
1px_999.gif
AC
 =c× AB
1px_999.gif
CA
以上から、AB=a+b× AB
1px_999.gif
BC
 +c× AB
1px_999.gif
CA
 …………＜4＞
とわかります。いま、a=12、b=54、c=6なので、
答えは、AB=12+54× AB
1px_999.gif
BC
 +c× AB
1px_999.gif
CA
 …………＜5＞

（2）
（1）で計算した＜4＞の式は、a,b,ｃの数値が変わっても用いることが出来ます。
＜2＞の条件のときは、ａ＝20、ｂ＝18、ｃ＝30なので、＜4＞の式にそれぞれを入れると、
AB=20+18× AB
1px_999.gif
BC
 +30× AB
1px_999.gif
CA
 …………＜6＞
が得られます。ここで、AB=80cmなので、＜5＞、＜6＞はそれぞれ、
54× AB
1px_999.gif
BC
 ＋6× AB
1px_999.gif
CA
 ＝80−12＝68…………＜7＞
18× AB
1px_999.gif
BC
 ＋30× AB
1px_999.gif
CA
 ＝80−20＝60…………＜8＞
となります。
＜7＞の式を5倍すると、
270× AB
1px_999.gif
BC
 ＋30× AB
1px_999.gif
CA
 ＝340…………＜9＞
となるので、＜9＞−＜8＞から、
AB
1px_999.gif
BC
 ＝（340−60）÷（270−18）＝ 10
1px_999.gif
9
また、この結果を＜7＞へ入れると、
AB
1px_999.gif
BC
 ＝（68−54× 10
1px_999.gif
9
 ）÷6＝ 4
1px_999.gif
3
答えは、 AB
1px_999.gif
BC
 ＝ 10
1px_999.gif
9
 　　 AB
1px_999.gif
CA
 ＝ 4
1px_999.gif
3

（3）
ＡＢ＝80と分かっているので、これを（2）の答えに入れます。
すると、答えは、
BC=80÷ 10
1px_999.gif
9
 ＝72（cm）、CA= 4
1px_999.gif
3
 ＝60（cm）


学習のポイント
この問題は算数の知識だけで解けますが、算数よりもむしろ数学の問題です。
ですので、解けた人はかなり自信を持って下さい。
さて、この問題のポイントはまず、補助線を引いて利用しやすい相似の図形を作ることです。補助線の引き方は様々ですので、苦手な人は代表的な問題にたくさんあたって下さい。
そして、㈬の式はａやｂの値が変化しても利用出来るということに注意して下さい。
この考え方は、実は高校に進んでからの数学で役に立つのです。
大変難しい問題でしたので、解けなくても落ち込む必要はありません。
解けた人も解けなかった人も、これからも勉強を頑張って下さい。
それでは、また来年！良いお年を！！
ギブアップ・ウィンドウを閉じる