■協力：東京出版 http://www.tokyo-s.jp/
毎月1日・11日・21日に問題解答を更新
11月12日／ハイレベル問題
【ギブアップ用解説】
（１） この様な問題で分からなくなったときは、まず、問題文の条件を図にしてみることが大切です。 問題文の条件をダイヤグラムに表すと下の図のようになります。

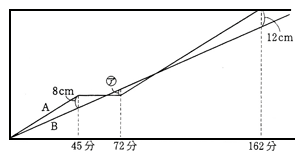
chart4.gif
始めの４５分間でＡの水面はＢの水面より８ｃｍ高くなっているので、７２分後から１６２分後までの９０分間ではＡの水面の上昇幅はＢの水面の上昇幅よりも１６ｃｍ高くなります。
つまり、ア＋１２＝１６
ア＝１６−１２＝４（ｃｍ）と分かります。
また、４５分後から７２分後までの間に注目すると、この２７分間で、Ｂの水面は８＋ア＝１２（ｃｍ）上がっていることが分かります。
つまり、２７分間でＢの水面は１２ｃｍ高くなることがわかります。
１６２分後に注目すると、Ｂの水面があと１２ｃｍ高くなればＢが満水になるので、あと２７分経てばＢが満水になると分かります。
よって求める時間は、１６２＋２７＝１８９（分後）
（2）
（１）より、Ｂの水面は２７分間で１２ｃｍ上がることが分かっているので、
Ｂの水面は毎分１２÷２７＝ 4
1px_999.gif
9
 （ｃｍ）上がります。
つまり、４５分間では、Ｂの水面は 4
1px_999.gif
9
 ×４５＝２０ｃｍ上がります。
４５分間ではＡの水面はＢの水面より８ｃｍ高く上がるので、４５分間でＡの水面は２０＋８＝２８（ｃｍ）上がることが分かります。
よって、Ａの水面は毎分２８÷４５＝ 28
1px_999.gif
45
 （ｃｍ）上がることが分かります。
また、Ａに水を入れた時間は全部で１６２−２７＝１３５分間なので、
Ａの水そうの高さは、 28
1px_999.gif
45
×１３５＝８４（ｃｍ）であると分かります。
Ａの水そうには、１３５分間水を入れたので、Ａの水そうの容積は１３５×１８９０＝２５５１５０（㎤）となります。 容積＝底面積×高さなので、
求める底面積＝５５１５０÷８４＝３０３７．５（㎠）

学習のポイント
この問題のポイントはダイヤグラムを作成して、Ａ，Ｂの水面の高さの上がる速度を比べることが重要です。 この問題の様に、しばらくの間、動きがとまるものが含まれている問題の場合、ダイヤグラムを書くことがポイントになることが多々あります。
ダイヤグラムを書けば、あとは相似などを利用してダイヤグラムの図を整理していけば問題は解けます。
この問題でつまづいた人は、ダイヤグラムの問題と、相似を利用した図の問題を復習しましょう。
ギブアップ・ウィンドウを閉じる