■協力：東京出版 http://www.tokyo-s.jp/

11月12日／プレ問題

【ギブアップ用解説】

三角形ＡＥＧとＥＢＦは、それぞれ辺ＡＥ、ＥＢを底辺と考えると高さが等しいので、 三角形ＡＥＧの面積：三角形ＡＢＦの面積＝＝◇：◇となり、三角形ＡＥＧの面積＝◇となります。
また、三角形ＡＥＧとＣＤＧは相似であり、辺ＤＣ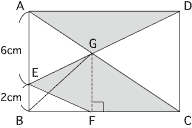＝＝◇なので、長さの比はとなるので、三角形ＡＥＧとＣＤＧの面積比は＝となり、三角形ＣＤＧの面積は◇となります。



さらに、三角形ＧＥＦとＧＢＦの面積は等しいので、図の網目部分の面積はの和と等しく、これは長方形ＡＢＣＤの面積の半分となります。
また、三角形ＥＢＦとＥＢＧの面積も等しいので、三角形ＡＥＧ、ＥＢＦ、ＤＣＧの面積の和は三角形ＡＥＧ、ＥＧＢ、ＤＣＧの面積の和と等しく、これも長方形ＡＢＣＤの面積の半分となります。
よって、求める面積＝＝＝◇㎠となります。


今回のポイントは３つです。
高さが等しい三角形は、面積の比が底辺の長さの比と等しくなること。
相似の図形の面積比を求められること。
底辺が共通で高さの等しい三角形の面積は等しくなること。
以上の３つです。
これらは、図形の面積の問題の肝となるポイントです。
どこかで、つまづいた人は、自分の定着していないポイントをしっかりと復習しましょう。

【穴埋め解答】
三角形ＡＥＧとＥＢＦは、それぞれ辺ＡＥ、ＥＢを底辺と考えると高さが等しいので、
三角形ＡＥＧの面積：三角形ＡＢＦの面積＝ＡＥ：ＥＢ＝３：１となり、三角形ＡＥＧの面積＝９となります。
また、三角形ＡＥＧとＣＤＧは相似であり、辺ＤＣ＝６＋２＝８なので、長さの比は３：４となるので、三角形ＡＥＧとＣＤＧの面積比は３×３：４×４＝９：１６となり、三角形ＣＤＧの面積は１６となります。
さらに、三角形ＧＥＦとＧＢＦの面積は等しいので、図の網目部分の面積は三角形ＡＧＤとＢＧＣの和と等しく、これは長方形ＡＢＣＤの面積の半分となります。
また、三角形ＥＢＦとＥＢＧの面積も等しいので、三角形ＡＥＧ、ＥＢＦ、ＤＣＧの面積の和は三角形ＡＥＧ、ＥＧＢ、ＤＣＧの面積の和と等しく、これも長方形ＡＢＣＤの面積の半分となります。
よって、求める面積＝三角形ＡＥＧ、ＥＢＦ、ＤＣＧの面積の和＝３＋９＋１６＝２８㎠となります。

---