|
(1)
|
ア、イ、カ、キのときをまとめて1つの図に表すと下図のようになります。
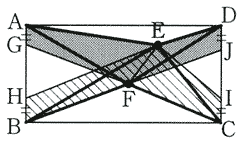
この図で、太線の四角形AFDEとBECFは面積が等しく、三角形AGFとDJFの面積の和と三角形HBEとICEの面積の和も等しいので、網目部分と斜線部分の面積が等しいことがわかります。
よって、求める面積は 127.5+132.5-172.5=87.5(㎠)
|
|
(2)
|
ク、ケ、コのとき、ウ、エ、オ、のときをそれぞれまとめて1つの図に表すと、下図のようになります。これらの図で、網目部分の面積はそれぞれ、クとコのとき、ウとオのときの面積の和です。
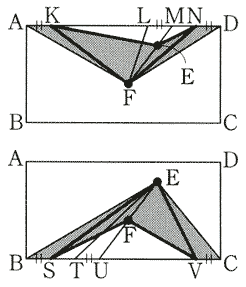
クとコのときの面積の和は、
三角形AFK+四角形KFNE+三角形NFD=四角形KFNE+三角形LFM×2=四角形KFNE+60(㎠)
ウとオのときの面積の和は、
三角形EBS+四角形ESFV+三角形EVC=四角形ESFV+三角形ETU×2=四角形ESFV+80(㎠)
であり、四角形KFNEとESFVの面積は等しいので、
ク+コ=ウ+オ-20(㎠)
とわかります。よって、求める面積は、
80+120-20-50=130(㎠)
|
|
(3)
|
アのときとイのときの三角形の面積の差
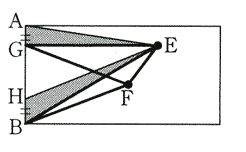
下図で網目部分の三角形の面積は等しいので、結局、アのときとイのときの面積の差に等しくなります。
172.5-127.5=45(㎠)………………………(☆)
コのときとウのときの三角形の面積の差
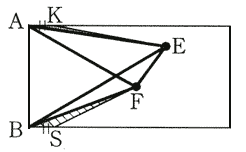
エのときはケのときよりも10㎠大きいので、下図の斜線部分の面積も網目部分の面積よりも10㎠大きくなります。よって、求める面積の差は、
130-(80-10)=60(㎠)………………………(★)
|
|
(4)
|
EFを底辺と見ると、(3)の(☆)と(★)はそれぞれ、
EF×BX÷2、
EF×BY÷2
で求められることになります。
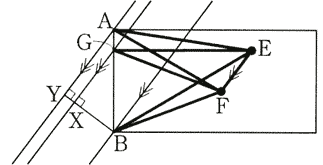
よって、BX:BY=45:60=3:4
となるので、相似形を利用して、
AB:GB=BY:BX=4:3
とわかります。したがって答えは、
AB:PQ=AB:AG=4:(4-3)=4:1
|



