|
(1)
|
|
(ⅰ)
|
(ⅰ)
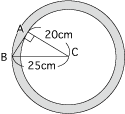
辺AB上で、Cから最も遠い点はB、最も近い点はAです。よって、点Cを中心にして三角形ABCを360度回転したときに、辺ABが通過する部分は、下図の網目部分です。よって求める面積は(25×25−20×20)×3.14=706.5(㎠)となります。


|
|
|
|
|
(ⅱ)
|
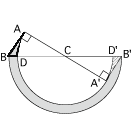
辺ABが通過する部分は、下図の網目部分です。ここで、太線部分を斜線部分に移すことにより、(ⅰ)の半分であることがわかります。つまり答えは706.5÷2=353.25(㎠)となります。


|
|
|
(2)
|
|
(ⅰ)
|
(1)と同じように考えて、点Aを中心にして三角形ABCを360度回転したとき、辺BCが通過する部分は、下図の網目部分です。

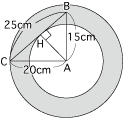

ここで、三角形ABCの面積を2通りに表すことにより、AH=20×15÷25=12(cm)とわかるので、求める面積は、(20×20−12×12)×3.14=803.84(㎠)
|
|
|
|
|
(ⅱ)
|
辺BCが通過する部分は、下図の網目部分です。ここで、太線部分を斜線部分に移すことにより、求める面積は(ⅰ)の半分よりも弓形BFの面積の分だけ大きいことがわかります。

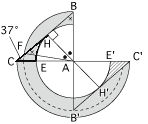

この弓形の面積は、おうぎ形ABFの面積から三角形ABFの面積を引くことで求められます。角BAFの大きさは、37×2=74(度)なので、おうぎ形ABFの面積は、
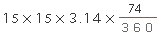 | =145.225(㎠)
|
また、三角形ABHとCBAの相似よりBH=15×12÷20=9(cm)なので、三角形ABFの面積は、(9×2)×12÷2=108(㎠)
以上から、求める面積は、803.84÷2+145.225−108=439.145(㎠)となります。
|
|



