|
(1)
|
|
(ⅰ)
|
分からなかったら、まず図を書いてみましょう。
図を書くと次の様になります。

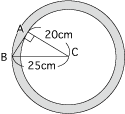

辺AB上で、Cから最も遠い点はBですので、辺CBが360度回転して出来るのが、図の外側の大きい円になります。
そして、辺AB上で、Cから最も近い点はAですので、辺CAが360度回転して出来るのが、図の内側の小さい円となります。
よって、点Cを中心にして三角形ABCを360度回転したときに、辺ABが通過する部分は、図の網目部分になります。
網目部分の面積は、図の大きい円の面積と小さい円の面積の差となりますので、
求める面積は、25×25×3.14−20×20×3.14=(25×25−20×20)×3.14=706.5(㎠)となります。
|
|
|
|
|
(ⅱ)
|
三角形ABCを180度回転させると、下図の様に三角形ABCは三角形A'B'Cの位置にまで移動します。

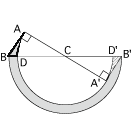

なので、辺ABが通過する部分は上図の網目部分となります。
ここで、図の太線部分と斜線部分は同じ図形なので、
網目部分の面積=網目部分の面積−太線部分の面積+斜線部分の面積
となります。
よって、求める面積は(ⅰ)の半分であることが分かります。
つまり、答えは、706.5÷2=353.25(㎠)となります。
|
|
|
(2)
|
|
(ⅰ)
|
(1)と同じやり方で考えます。
辺BC上で、Aから最も遠い点はCです。
そして、辺BC上で、Aから最も近い点は、Aから辺BCに垂直に下ろした点で、その点を下図の様にHとします。



また、ここで、AHの長さについて考えます。
三角形ABCの面積はAB×AC÷2ですが、BC×AH÷2とも表すことが出来ます。
つまり、AB×AC÷2=BC×AH÷2
AB×AC=BC×AH
AH=AB×AC÷BC=15×20÷25=12(cm)となります。
また、(1)と同じ様に考えて、点Aを中心にして三角形ABCを360度回転したとき、辺BCが通過する部分は、下図の網目部分となります。

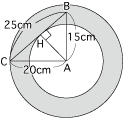

よって、求める面積は、半径ACの外側の大きい円と半径AHの内側の小さい円との面積の差となるので、
求める面積は、20×20×3.14−12×12×3.14=(20×20−12×12)×3.14=803.84(㎠)となります。
|
|
|
|
|
(ⅱ)
|
点Aを中心にして、三角形ABCを180度回転させると、下図の三角形AB'C'の位置まで移動します。

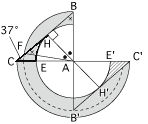

よって、辺BCが通過する面積は上図の網目部分となります。
ここで、太線部分と斜線部分の面積は同じなので、(1)と同じ様に考えて、
網目部分の面積=網目部分の面積−太線部分の面積+斜線部分の面積
となるので、求める面積は、(ⅰ)の半分+(おうぎ形ABFの面積−三角形ABFの面積)となります。
また、角度BAH=180°−角度BHA−角度ABH
=180°−90°−角度ABH
=180°−角度BAC−角度ABC=角度ACB=37°となります。
したがって、角度BAH=角度ACBなので、三角形ABCと三角形HBAはそれぞれの角度が等しくて相似となります。
よって、AC:AB=HA:HBつまり、20:15=12:HBとなり、
15×12=HB×20
HB=15×12÷20=9(cm)となります。
さらに、三角形AHBと三角形AHFは合同なので、
BF=BH×2=18(cm)、角度BAF=角度BAH×2=74°となり、
三角形ABFの面積=BF×AH÷2=18×12÷2=108(㎠)
|
おうぎ形ABFの面積= | 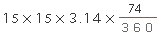 |
=145.225(㎠) |
となります。
以上から求める面積は803.84÷2+145.225−108=439.145(㎠)となります。
|
|






