|
�w�����o�ŕҏW���x
���ڂ̉ߋ��� �E�C�钆�w�����w�Z �E���w�@��w�v��R���w�����w�Z �E���M���w�Z�E�����w�Z �E���֒��w�Z�E�����w�Z �E�Ջ����w�E�����w�Z  |
���x�����Ńt�F�A�Ȑ��_��������
�u�V�����a�m�v����� �C��
���w�����w�Z 

�@���@ ��ʇ@ 6
�@�@�}�̂悤�ȗ����̂ɂ�����, ��BC, CD�̂܂̓_�����ꂼ��M, N�Ƃ��܂��B �@�@�܂�, AM��BN �������_��P�Ƃ��܂��B 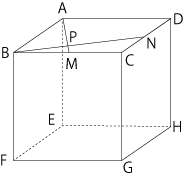 �@�@���̂Ƃ�, �O�p�`PBM�̖ʐς�$7\dfrac{1}{5}$cm2�ƂȂ�܂����B
�@�@���̂Ƃ�, �O�p�`PBM�̖ʐς�$7\dfrac{1}{5}$cm2�ƂȂ�܂����B�@�i�P�j�����̂�1�ӂ̒��������߂Ȃ����B �@�i�Q�j3�_A, F, M��ʂ镽�ʂ�, 3�_B, G, N ��ʂ� �@�@�@�@���ʂł��̗����̂�ؒf����Ƃ�, �_H���܂ޗ��̂� �@�@�@�@�̐ς����߂Ȃ����B ��@�̃|�C���g
�����̂�2�����ł��B���ʕ����𐳂����Ƃ炦, �̐ς����߂܂��傤�B
�E���
�i�P�jBN�̉�����AD�̉����̌�_��Q�Ƃ��܂��B
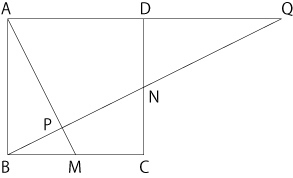 �@�O�p�`BCN��QDN�͍����ł��邱�Ƃɒ��ڂ����,
�@�O�p�`BCN��QDN�͍����ł��邱�Ƃɒ��ڂ����, �@AP�FPM��AQ�FBM�� �@AD$�~$2�FBC$��$2��4�F1 �@�����, �O�p�`ABM�̖ʐς�, �@�O�p�`ABM�̖ʐς�, �@AB$�~$�iAB$��$2�j$��$2��AB$�~$AB$��$4 �ŋ��߂��, ���ꂪ36cm2�Ȃ̂�, �@�@AB$�~$AB��36$�~$4��6$�~$6$�~$2$�~$2 �@��12$�~$12�icm2�j �Ƃ킩��܂��B����ē�����12cm�ł��B �i�Q�jA, F, M��ʂ镽�ʂŐؒf����ƎO�p�����l-ABF��, B, G, N��ʂ镽�ʂŐؒf����ƎO�p����N-BCG�����ꂼ�ꗧ���̂�������܂��B����2�̎O�p�����̋��ʕ�����, �E�}��
���w�Z�̃z�[���y�[�W�����p���悤�I
�u������Ɛt�v��, ���������͂�
���w�@��w�v��R
���w�����w�Z 

�@���@ ST��1�� �y3�z
�@����̖ʂ͔��F, ��������̖ʂ͐ԐF��100���̃J�[�h������܂��B�����̃J�[�h ������1���@1�̔{����������Ă���J�[�h�����ׂĂЂ�����Ԃ� �E
������99���@99�̔{����������Ă���J�[�h�����ׂĂЂ� ����Ԃ��E �E ������100�� 100�̔{����������Ă���J�[�h�����ׂĂЂ�����Ԃ� �@���ׂẴJ�[�h�𔒐F�̖ʂ���ɂ��Ă���, ������n�߂܂��B���̖₢�ɓ����� �i�P�j������18���������s�Ȃ����Ƃ�, �ԐF�̖ʂ���ɂȂ�J�[�h�͉�������� �i�Q�j������1�����灃����100���܂ŏ��ɂ��ׂĂ̑�����s�Ȃ����Ƃ�, 20�� �i�R�j������1�����灃����100���܂ŏ��ɂ��ׂĂ̑�����s�Ȃ����Ƃ�, 1 ���� �i�S�j������2���Ɓ�����3�����������ɍs�Ȃ�������, �ԐF�̖ʂ���ɂȂ�J�[�h �i�T�j������1�����灃����100���܂ŏ��ɂ��ׂĂ̑�����s�Ȃ�������, �ԐF�� ��@�̃|�C���g
�̌��Ɍ��т��čl�������, ���܂��܂Ȓ��w�Z�ŗޑ肪�o�肳��Ă��܂��B
�E���
�i�P�j100$��$18��5�]��10 ���w�Ȏ�C �O�� �M�V�搶�̃R�����g
����\�������, �������\�͂̈琬��ڕW�Ƃ���
�@�{�Z�ł͌v�Z�͂Ǝv�l�͂���ނ��Ƃ�ڕW�ɂ���, �����i�K�ɉ��������g�݂��s���Ă��܂��B
�@���w�ł͊�b�I�Ȍv�Z�͂�g�ɕt������悤��, �v�Z�͐f�f�e�X�g���J��Ԃ����{���Ă��܂��B�܂�, ��2����͐}�`�̏ؖ��ȂǂŔ��z�́E�\���͂�, �����Ē�3����͍��Z�̓��e����肵, �e�P����ʂ��Ďv�l�͂��{���Ă����܂��B �@�l�X�Ȋp�x���������, ���ɑg�ݍ��킹�邱�Ƃɂ���Ė��������ق����Ă����B���w�̖��������Ȃ���, �_���I�v�l��g�ɕt���ė~�����ƍl���Ă��܂��B ���w�Z�̃z�[���y�[�W�����p���悤�I
����Ɨ��̋C�T�ƉȊw�I���_��
����̃��[�_�[�ƂȂ� ���M
���w�Z�E�����w�Z 

�@���@ 3
�@ 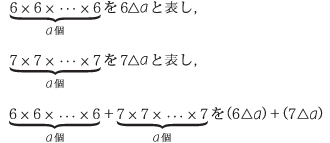
�ƕ\�����Ƃɂ��܂��B������, 6��1��6, 7��1��7�Ƃ��܂��B �@���̖₢�ɓ����Ȃ����B������, �ꂯ���̐��̏\�̈ʂ̐�����0�Ƃ��܂��B �i�P�j �i�Q�j7��2018�̏\�̈ʂ̐������߂Ȃ����B �i�R�j6��2018�̏\�̈ʂ̐������߂Ȃ����B �i�S�j�i6�� ��@�̃|�C���g
�]��̎������Ɋւ���K�����̖��ł��B��������Ⓑ���ł���, �Ă��˂��ɏ����o���܂��傤�B
�E���
�i�P�j7��
�@�����̏\�̈ʂ̐��������ƂȂ�܂��B
���, 2�Ԗڂ�49�̏\�̈ʂ�4�ł��B �i�R�j�U��
��5��1�g�̎����ƂȂ��Ă��܂��B�����, ���߂鐔��,�i2018�|1�j$��$5��403�E�E�E2 ���, 2�Ԗڂ�16�̏\�̈ʂ�1�ł��B �i�S�j�i�P�j�`�i�R�j���, 7�� �@ �@
�i2018�|1�j$��$20��100�E�E�E17���, �\��17�ڂ� ���w�Ȏ�C ���� ���F�搶�̃R�����g
���含����m������, ��̐��w
�@���M�̐��w��, ����w�Ԏp�����m�����邽�߂�, �u�\�K���Ď��ƂɗՂށv�Ƃ������Ƃ��w���̒��Ƃ��Ă��܂��B
�@���w1�E2�N��2�N�ԂŒ��w�ے���, ���w3�N���獂�Z2�N�܂ł�3�N�Ԃō��Z�ے����C����, ���Z3�N�ł͖�艉�K�𒆐S�Ƃ������ƂƂȂ��w�����̏��������܂��B �@�i�x���͂₭�������J���L�������ɑΉ����邽�߂�, �����w�N�ɂ�����, �N���X��2�ɕ��������l���������Ɓi���k��l�ЂƂ�ɑ��鉉�K�ʂ𑝂₵, �Y�폕�����邱�Ƃɂ��, �v�Z��, �}�`�ւ̒��ϗ�, �_�ؗ͂�g�ɂ�����Ɓj�����{���Ă��܂��B �@���������Ƃ���, ���Ɖ��M���g����, �����̍l������}�ŕ\������, �v�Z��������Ə������Ƃ���n�߂܂��傤�B ���w�Z�̃z�[���y�[�W�����p���悤�I
�]�����E�傫���E�L���ɁE�[���]
����
���w�Z�E�����w�Z 

�@���@ B���� 5
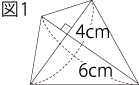 �@���̊e�₢�ɓ����Ȃ����B
�@���̊e�₢�ɓ����Ȃ����B�i�P�j�}1�̎l�p�`�̖ʐς͉�cm2�ł����B 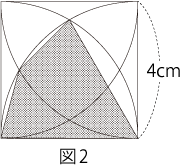 �i�Q�j�}2��1�ӂ�4cm�̐����`��, �e���_�𒆐S�Ƃ������a4cm�̉~�̈ꕔ��, �������������������̂ł��B
�i�Q�j�}2��1�ӂ�4cm�̐����`��, �e���_�𒆐S�Ƃ������a4cm�̉~�̈ꕔ��, �������������������̂ł��B �i�R�j�}3��1�ӂ�4cm�̐����`ABCD��, �e���_�𒆐S�Ƃ������a4cm�̉~��, �������������������̂ł��B
�i�R�j�}3��1�ӂ�4cm�̐����`ABCD��, �e���_�𒆐S�Ƃ������a4cm�̉~��, �������������������̂ł��B�@�Ԗڕ����̖ʐς̘a�͉�cm2�ł����B ��@�̃|�C���g
�u����Ȗʐ�, �Z���ŋ��܂�́H�v�Ǝv����������܂���B�U�������܂�����Ă��܂��̂�, ���Ђ��̗���ɏ��܂��傤�B
�E���
���w�Ȏ�C �ˎ� ��搶�̃R�����g
���w���̂��̖̂��͂ɋC�t������܂�
�@���w�͕��n�E���n�ɊW�Ȃ�, ���_�I�ɍl���ؖ�����Ƃ���, ���Љ�Ŗ𗧂\�͂���ދ��Ȃł��B�Z���Ƃ͈قȂ�, �����ɂ��ǂ蒅���ߒ��̕����d������܂��B
�@���Z�ߒ��ł͏K�n�x�ʎ��Ƃ�R�[�X��������������Ă���̂�, �����������т␔�w�̊y�����𖡂킦����������Ă��܂��B���Ƃł͂��������m�[�g�Ɏʂ��̂ł͂Ȃ�, �����ōl���Đ������w�͂����Ă��������B��������Α�w����Љ�l�ɂȂ�����, ���w����i�Ƃ��Ē�R�Ȃ��p���邱�Ƃ��ł���悤�ɂȂ�, �X�ɂ͐��w���̂��̖̂��͂ɋC�Â��͂��ł��B ���w�Z�̃z�[���y�[�W�����p���悤�I
6�N�ԂŐg�ɂ��鎩�M�ƌւ�
�Ջ�
���w�E�����w�Z 

�@���@ ��3�� 6
�@1200m 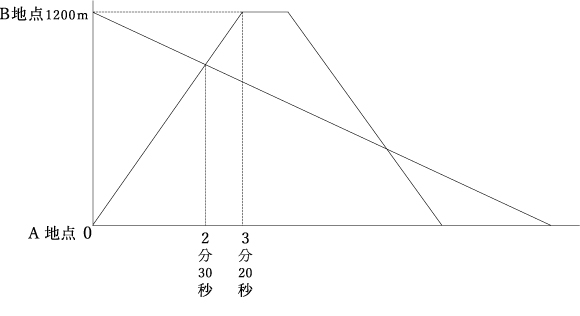 �i�P�j���Y�N�̎��]�Ԃ̑����͖�����m�ł����B �i�Q�j���Y�N�̃W���M���O�̑����͖�����m�ł����B �i�R�j���Y�N��, B�n�_����A�n�_�ɖ߂� �@�@�@�������b��ł����B �i�S�j���Y�N��B�n�_�ł̋x�������Ԃ�����ς���, 2�l��������A�n�_�� �@�@�@�܂��B���Y�N�̋x�������Ԃ��������b�ɂ���悢�ł����B ��@�̃|�C���g
�O���t�̓ǂݎ�������߂������̖��ł��B������܂��g���čl���܂��傤�B
�E���
�i�P�j���Y��3��20�b��1200m�i�̂�,
�@�@$1200��3\dfrac{20}{60}$��360�im/���j �i�Q�j1200m�̓��̂��i�ނ̂ɂ����鎞�Ԃ�, ���Y�݂̂���3��20�b, ���Y�Ǝ��Y��2�l����2��30�b�ł��B �@�@3��20�b�F2��30�b=200�b�F150�b��4�F3 �Ȃ̂�, �����̔��, ���̋t��� �@�@���Y�F�i���Y�{���Y�j��3�F4 �ł��B�����, �����̔�� �@�@���Y�F���Y=3�F�i4�|3�j��3�F1 �Ȃ̂�, ���Y�̑����� �@�@$360�~\dfrac{1}{3}$��120�im/���j �i�R�jB�n�_����ǂ������n�_�܂Ői�ނ̂ɂ����鎞�Ԃ̔��, �����̋t��� �@�@���Y�F���Y��1�F3 �ł��B���Y���x�������I����̂��o�����Ă���4��20�b��Ȃ̂�, �@�@$4��20�b�~\dfrac{3}{3-1}$��6��30�b ���, 6��30�b���ł��B �i�S�j���Y��A�n�_�ɓ�������̂�, �o�����Ă��� �@�@1200$��$120��10�i����j �ł��B���Y���������̓��̂��i�ނ̂ɂ����鎞�Ԃ� �@�@3��20�b$�~$2��6��40�b �Ȃ̂�, �@�@10���|6��40�b��3��20�b ���w�Ȏ�C �c�� ��G�搶�̃R�����g
���������߂邾���łȂ�, ���߂�ߒ����d������
�@�{�Z�ł͎��Ƃ�ʂ��Đ��w�̊�{�m���̒蒅��}���, ���W�I�Ȗ�����������, ���̂��܂��܂ȉ������ɐG���@��������Ă��܂��B
�@���Ƃ͐搶�Ɛ��k������肵�Ȃ���i��ł����܂��B���w�̖��͓��������߂�܂ł̉ߒ����l���ĉ����Ă����܂���, ���ɂ���Ă͉�����������������܂��B�����̉����������ƂŏЉ����, �������ɂ��Ĉӌ����o�������Ă��炤��ʂ�����܂��B �@���܂��܂ȉ��������l����Ƃ���ɐ��w�̑�햡������܂��B�����Ջ��ł�������ɐ��w�̑�햡�𖡂킢�܂��傤�B ���w�Z�̃z�[���y�[�W�����p���悤�I
|
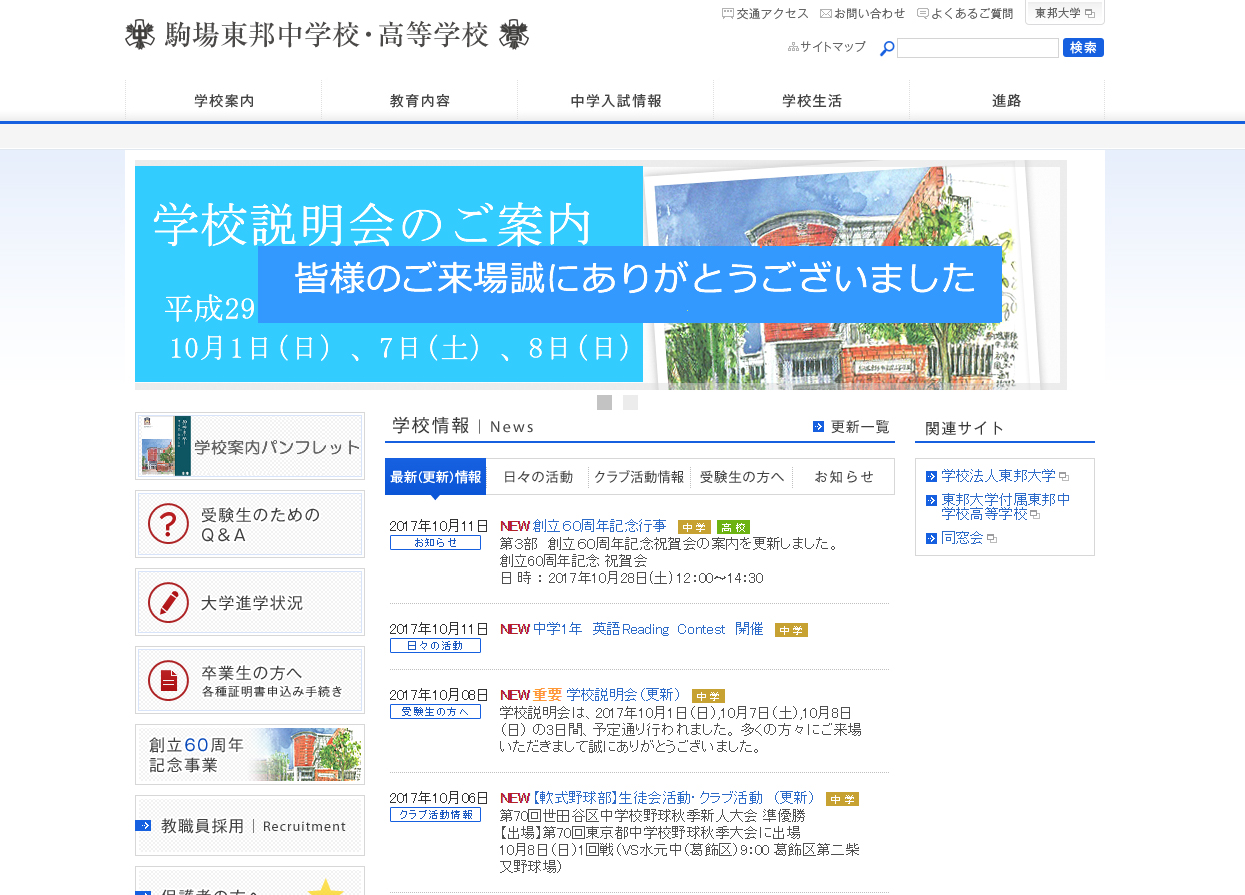
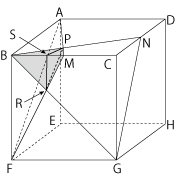 �@���̖Ԗڕ����̎O�p�����̑̐ς�, �O�p�`PSR���ʂƂ�, ������BM��6cm�̎O�p�����̑̐ςƂ��ċ��߂��܂��B
�@���̖Ԗڕ����̎O�p�����̑̐ς�, �O�p�`PSR���ʂƂ�, ������BM��6cm�̎O�p�����̑̐ςƂ��ċ��߂��܂��B
 �i�P�j4$�~$6$��$2��12�icm2�j
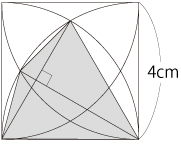
�i�P�j4$�~$6$��$2��12�icm2�j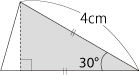 �ӎO�p�`2���ƍl���Ă������܂��B�Ԗڕ����̒��p�O�p�`�����O�p�`�����傤�ǔ����ɂ����`�ł��邱�Ƃ���, 4cm�̕ӂ��ӂƎv�����Ƃ��̍�����4cm�̔�����2cm�ł��B�����,
�ӎO�p�`2���ƍl���Ă������܂��B�Ԗڕ����̒��p�O�p�`�����O�p�`�����傤�ǔ����ɂ����`�ł��邱�Ƃ���, 4cm�̕ӂ��ӂƎv�����Ƃ��̍�����4cm�̔�����2cm�ł��B�����,  �i�R�j�E�}�̂悤��, �����̐����`��Ίp���Ŏl�������܂��B���̒��p�ӎO�p�`OPQ�ƊO����1��4cm�̐��O�p�`�̖ʐς̘a��, ���߂�ʐς�$\dfrac{1}{4}$�ɂȂ�܂��B
�i�R�j�E�}�̂悤��, �����̐����`��Ίp���Ŏl�������܂��B���̒��p�ӎO�p�`OPQ�ƊO����1��4cm�̐��O�p�`�̖ʐς̘a��, ���߂�ʐς�$\dfrac{1}{4}$�ɂȂ�܂��B

�@�o�������ɂ��Ă͂��ꂾ���Ŗ�������, �ł��Ȃ������F�B���u�Ȃ�قǁv�Ɣ[������������N���ł��邩�ǂ��������⎩�����Ă��������B
�@�o���Ȃ���肪�����Ă��Q���͖��p�ł��B���w�����̎Z���̏o��̔w�i�ɂ�, �����̐�l�����̉p�m�����W���Ă���̂ł��B�u�Ȃ�ق�, ����Ȃ�ł��Ȃ����Ƃ�����ȁv�ƃ����b�N�X����, ��l�Ɍh�ӂ�\���g������ӏ܁h����C����, ���̕M�����������ł���������邩���y���݂Ȃ��猟�����邱�Ƃ��N�̍��Y�ƂȂ�ł��傤�B
�@�C��́g�D��S�ƔS��h���������F����ɉ����鐔�w��W�J���܂��B�N�̓��w��҂��Ă��܂��B