(2)までは落とせません。(3)で勝負です。
[解説] 435=3×5×29……………………(★)
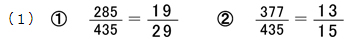
(2)★より,既約分数の分子は,3でも5でも29でも割り切れない数 (…☆) です。
そこで,1から★までの整数で,
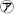
3の倍数,5の倍数,29の倍数
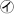
3,5,29のうちの2数の公倍数である
3×5の倍数,3×29の倍数,5×29の倍数
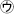
3数の公倍数である3×5×29の倍数
の個数 (★÷3,★÷5,…などの,割り算の商です) を調べると,順に,
145個,87個,15個
29個,5個,3個
1個
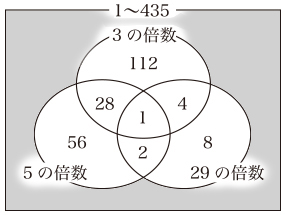
となるので,これをベン図に表すと,右のようになります。
求めるものは,図の
網目部分に入る数の個数ですから,答えは,
435−(145+56+8+2)=
224 (個)
⇒注 少し高度ですが,本問には
背景があります。
1から435までの整数を,
3で割った余りをa (a=0,1,2),
5で割った余りをb (b=0,1,2,3,4),
29で割った余りをc (c=0,1,2,…,28)
とすると,異なるa,b,cの組は,
3×5×29=435 (通り) 考えられますが,これらの1つ1つが435個の整数のそれぞれに
1対1に対応します。
かりに,等しい組が対応する2数m,n (m>n)が存在するとすれば,435より小さい
m−nが435で割り切れることになり,
矛盾するからです。
以上から,☆の個数は,0と異なるa,b,cの組の数で,2×4×28=
224 (個)
(3)1から15までの数が,3で割れる (○)か割れない (×) か,5で割れるか割れないかを調べると,下表のようになり,以後,この○,×の分布は
繰り返されます。
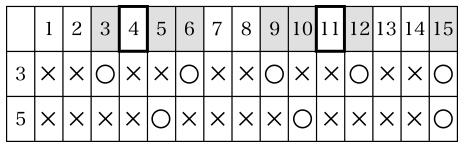
29を考えない時点では,網目部分が既約分数
ではない分数の分子です。
さて,この○,×の分布の連続の中に,29で割れるか割れないかの○,×の帯
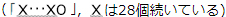
を重ねると,○のつく数,つまり29の倍数が,表の太線
枠にきたとき,左右の網目部分と合わせて4つ,網目が続くことになります。
これが,網目部分が最も長く続く場合です。
太線枠には,4を引くか足すと15の倍数となる数が入りますから,29の倍数の中からそのような数を探すと,116と319が見つかります。
よって答えは,
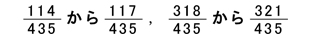
出来た問題についてはそれだけで満足せず、できなかった友達が「なるほど」と納得する説明を君ができるかどうかを自問自答してください。
出来ない問題があっても嘆きは無用です。中学入試の算数の出題の背景には、多くの先人たちの英知が結集しているのです。「なるほど、それならできないこともあるな」とリラックスして、先人に敬意を表しつつ“名画を鑑賞”する気分で、その筆遣いを少しでも取り入れられるかを楽しみながら検討することが君の財産となるでしょう。
海城は“好奇心と粘り”をもった皆さんに応える数学を展開します。君の入学を待っています。