�@�~�ɓ��ڂ��鐳�Z�p�`���v���o���ƁA�����`�͉~����Z��������_������ł������Ƃ�������܂��B
�i1�j���}�̂悤�ɂȂ�܂��B
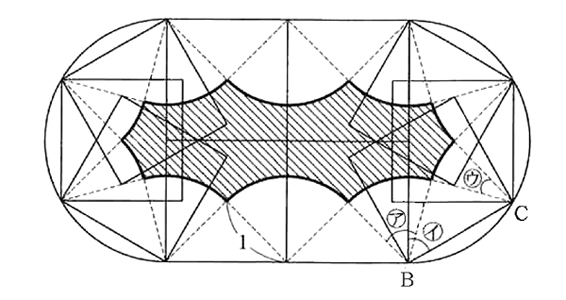
�i2�j�C�͐��Z�p�`��1�̓��p(120��)�̔����Ȃ̂�60���ł��BB�𒆐S�ɐ����`��60����]���邱�Ƃ�\���Ă���̂ŁA
�A��60���ł��B
�@�E��120���|45���~2��30���Ȃ̂ŁA�����`��C�𒆐S��30����]���܂��B
�@�ʐς�2cm
2�̐����`�̑Ίp���̒�����2cm�ł�����A�}�̂������`�̔��a��1cm�ł��B
�@�������`�̒��S�p�̑��a�́A
�@�@90���~2�{60���~4�{30���~4��540��
�@�}�`�̎���̒����́A
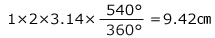
�i3�j���a1 cm�A���S�p540�����̂������`�ƁA�ʐς�2 cm
2�̐����`��4����1�̒��p�ӎO�p�`��10�Ȃ̂ŁA���߂�ʐς́A
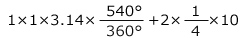
=9.71(cm
2)
�@�o�������ɂ��Ă͂��ꂾ���Ŗ��������A�ł��Ȃ������F�B���u�Ȃ�قǁv�Ɣ[������������N���ł��邩�ǂ��������⎩�����Ă��������B
�@�o���Ȃ���肪�����Ă��Q���͖��p�ł��B���w�����̎Z���̏o��̔w�i�ɂ́A�����̐�l�����̉p�m�����W���Ă���̂ł��B�u�Ȃ�قǁA����Ȃ�ł��Ȃ����Ƃ�����ȁv�ƃ����b�N�X���āA��l�Ɍh�ӂ�\���g������ӏ܁h����C���ŁA���̕M�����������ł���������邩���y���݂Ȃ��猟�����邱�Ƃ��N�̍��Y�ƂȂ�ł��傤�B
�@�C��́g�D��S�ƔS��h���������F����ɉ����鐔�w��W�J���܂��B�N�̓��w��҂��Ă��܂��B